Question
(a) Calculate the magnitude of the acceleration due to
gravity on the surface of Earth due to the Moon.
(b) Calculate the magnitude of the acceleration due to gravity at Earth due to the Sun.
(c) Take the ratio of the Moon's acceleration to the Sun's and comment on why the tides are predominantly due to the Moon in spite of this number.
Final Answer
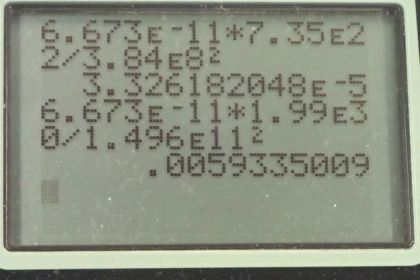
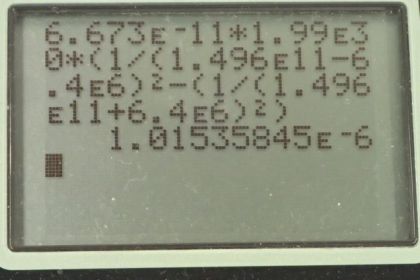
- The acceleration due to gravity on the Earth's surface due to the sun is 178 times that due to the moon. The tides are cased by the difference in gravitational force between the near and far sides of the Earth. The difference for the moon is whereas for the sun the difference is . The difference due to the sun is about half that due to the moon, which is still significant enough to manifest as spring tides every two weeks when the sun-Earth-moon line up.
Solution video
OpenStax College Physics for AP® Courses, Chapter 6, Problem 34 (Problems & Exercises)

vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. We are going to calculate the acceleration due to gravity on the surface of the Earth due to the Moon in part (a) and then due to the Sun in part (b) and then we are gonna talk about how you know, those two differ and that of the Sun is a lot larger but why do the tides predominantly become affected by the Moon instead of the Sun given that the Sun has such a much greater force, or greater acceleration due to the Sun on the surface of the Earth. So we'll talk about that... has more to do with the difference than the actual amount but one thing at a time. So the acceleration on the surface of the Earth due to the Moon: gravitational constant multiplied by the mass of the Moon divided by the average distance between the Earth and the Moon squared. So all these numbers I looked up before starting the question of course you always wanna write down the information that you know or need and here's gravitational constant times mass of the Moon divided by the Earth-Moon distance squared giving 3.33 times 10 to the minus 5 meters per second squared. And then for the Sun, it's the same formula but with the Sun's mass and the Earth-Sun distance on average squared and that gives 5.93 times 10 to the minus 3 meters per second squared. So taking a ratio of the acceleration due to the Sun on the Earth's surface and then to that of the Moon gives about 178. So the acceleration on the surface of the Earth due to the Sun is 178 times as much as that of the Moon. But tides are not caused by the amount of gravitational force, they are caused by a difference in the gravitational force between the near and far sides of the Earth. So the Moon is a lot closer to the Earth and that causes the difference between the acceleration due to the Moon on the surface of the Earth on the near side to be a lot different than on the far side. So you can imagine that the water that's here is being accelerated towards the Moon and likewise the Earth itself is being accelerated towards the Moon but I should draw this arrow a little bit shorter because I wanna illustrate how as you get farther from the Moon this force is reduced and it's this change in the force that causes a stretching of this whole body— the body being this water-Earth system— and as it gets stretched out, it bulges on this side and it also bulges on the back side and you can imagine that the Earth itself is being pulled to the right accelerated to the right away from this water that's on the back side and so it just hangs off the end being left behind. Okay! And I'll show you with numbers how the difference in acceleration due to the Moon on the surface of the Earth on the near side versus the far side is greater than the difference for the Sun. So here we have: acceleration on the near side is the Earth-moon distance which is from center to center— that's how these distances are typically measured— and then we are gonna subtract the radius of the Earth from the distance here so that's the near side acceleration and then to find the far side, we'll add the Earth's radius to this center-to-center Earth-Moon distance. And we can factor out this g and the mass of the Moon and then so on and so on... plug in numbers. So we are subtracting the Earth's radius and then adding the Earth's radius to this Earth-Moon distance and we end up with 2.2 times 10 to the minus 6 meters per second squared is the difference in acceleration due to gravity on the near versus far side due to the Moon. And then for the Sun, we have the Sun's mass here and we have the Earth-Sun distance minus the Earth radius and then Earth-Sun distance plus the Earth radius and we get 1.0 times 10 to the minus 6 meters per second squared. So this number is about half of that but it's nevertheless still big and there are in fact solar tides. So the Sun does cause some of the tides but you don't really notice it very much because the Moon has a bigger effect. But where you do notice the Sun's effect is when the Moon and the Sun line up. So these are called spring tides and they occur about every 2 weeks at full and new moons. And when you have a full moon, you have the Moon here and you have Earth here and then the Sun's over here and they all line up. And this being the dark side of the Earth, you see this bright Moon here or it also happens during new moons in which case the Moon is is here and you are on the dark side of the Earth and you don't see any Moon at all because the Moon's over here on the bright side of the Earth. Okay so that's the story!