Question
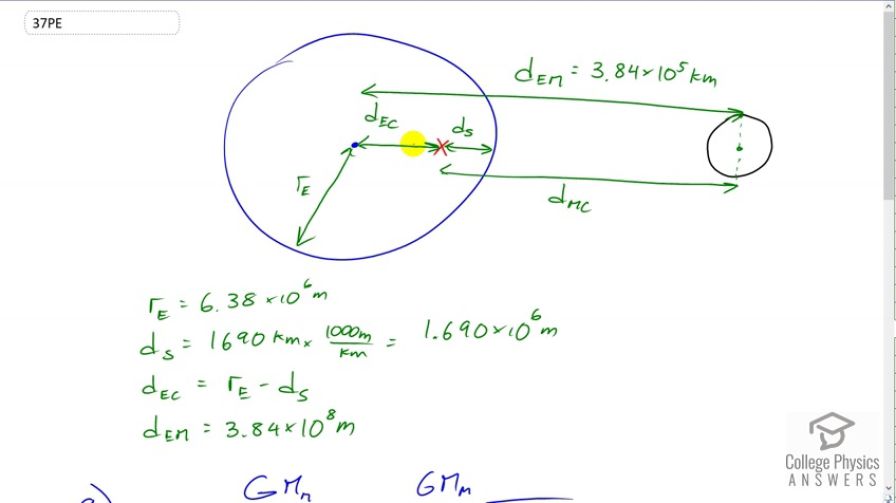
The Moon and Earth rotate about their common center of mass, which is located about 4700 km from the center of Earth. (This is 1690 km below the surface.)
(a) Calculate the magnitude of the acceleration due to the Moon's gravity at that point.
(b) Calculate the magnitude of the centripetal acceleration of the center of Earth as it rotates about that point once each lunar month (about 27.3 d) and compare it with the acceleration found in part (a). Comment on whether or not they are equal and why they should or should not be.
Final Answer
a)
b) . These are nearly equal, which is expected since the moon is providing the centripetal force which causes the Earth's center to rotate about the center of mass of the Earth-Moon system.
Solution video
OpenStax College Physics for AP® Courses, Chapter 6, Problem 37 (Problems & Exercises)
vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. The center of the earth is slowly rotating around this point here which is the center of mass between the earth and the moon. It takes 27.3 days approximately, one lunar month, for this geometric center of the earth to go around the center of mass that's here at the red x. Now the moon is what's providing the centripetal force to make this happen and we're going to find out that the acceleration due to gravity of the moon at this position, which is 3.41 times ten to the minus five meters per second squared, is pretty much the same as the centripetal acceleration of the center of the earth around this point which we calculate to be 3.33 times ten to the minus five meters per second squared. These numbers are nearly the same and this is what we expect because the earth-- oh sorry -- the moon is what's providing the centripetal force to make this centripetal acceleration happen around the center of mass. Okay. So part A of this question asks to calculate the magnitude of the acceleration to the moon's gravity at this position here. So we have to set up our geometry properly. We know what the radius of the earth is, that's something we can look up in the data table, 6.38 times ten to the six meters and we're told that the center of mass is a distance below the surface of the earth, 1690 kilometers which we convert into meters, 1.69 times ten to the six meters. We know the earth moon distance which is center to center, that's 3.84 times ten to the five kilometers which we can look up in the data table. We'll take that number and then minus this earth center to center of mass distance to figure out the distance from the moon center to the center of mass. So -- oops, let's put that back there -- so this is what we have down here. We have the acceleration due to gravity of the moon at the center of mass equals the gravitational constant multiplied by the mass of the moon, divided by this distance from the center of the moon to the center of mass between the earth and the moon. So that's the distance from the earth to the moon minus this distance here. This distance here is the radius of the earth minus the distance below the surface of the earth to the center of mass. That's what we have here. So, we have 6.673 times ten to the minus eleven times mass of the moon, 7.35 times ten to the twenty-two kilograms, divided by the distance from the center of the moon to the center of the earth and then take away this bit of distance between the center of the earth and the center of mass, which is the radius of the earth, take away the distance below the surface of the earth. Then we square that result there and then we get 3.41 times ten to the minus five meters per second squared is the acceleration due to gravity of the moon. Now the centripetal acceleration of the center of the earth around that center of mass is the distance from the center of the earth to the center of mass, multiplied by the angular velocity squared. The angular velocity we can find by taking two pi radians because the center of mass of the earth does a full circle two pi radians in 27.3 days. But we have to convert those days into seconds in order to use it in this formula. So we have 27.3 days times 24 hours per day, and then the days cancel, and then multiply by 3600 seconds per hour and then we have seconds at the bottom. So this is the radius of the earth minus the distance below the earth's surface to the center of mass and working this all out, that works to 3.33 times ten to the minus five meters per second squared.
