Question
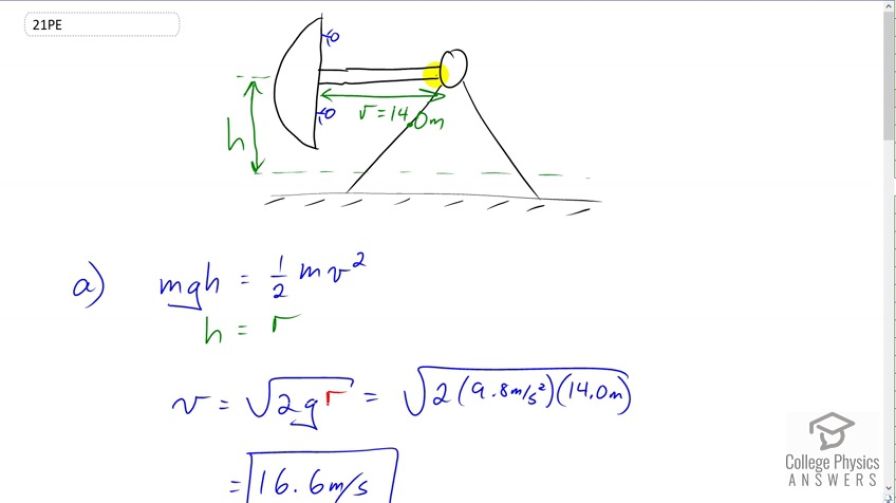
Riders in an amusement park ride shaped like a Viking ship hung from a large pivot are rotated back and forth like a rigid pendulum. Sometime near the middle of the ride, the ship is momentarily motionless at the top of its circular arc. The ship then swings down under the influence of gravity.
- Assuming negligible friction, find the speed of the riders at the bottom of its arc, given the system's center of mass travels in an arc having a radius of 14.0 m and the riders are near the center of mass.
- What is the centripetal acceleration at the bottom of the arc?
- Draw a free body diagram of the forces acting on a rider at the bottom of the arc.
- Find the force exerted by the ride on a 60.0 kg rider and compare it to her weight.
- Discuss whether the answer seems reasonable.
Final Answer
a)
b)
c) , is greater than by a factor of 3.
d) Yes, this is reasonable since it shoudl be greater than in order to accelerate the rider upwards, but not so much greater as to cause injury.
Solution video
OpenStax College Physics for AP® Courses, Chapter 6, Problem 21 (Problems & Exercises)
vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. This amusement park ride consists of a ship with people sitting in it and it's connected by a rigid beam to this pivot here and the boat goes back and forth like this. Now, at the bottom of its arc we're going to figure out what its linear speed is there. We'll also find the centripetal acceleration at that point and draw a free body diagram and then figure out what is the force with which the ride is pushing up on the rider at the bottom of the arc. Now you're meant to know a little bit from a chapter you haven't gotten to yet, which is that potential energy at this point where the ride is stationary and we assume that it becomes stationary at a point that's horizontal. I mean we have to assume something, so let's make that assumption. So the concept is that the potential energy at this horizontal position here its maximum height, turns into kinetic energy by the time it gets down here. This potential energy here is entirely turned into kinetic energy at the bottom of its travel because we've taken the bottom of its travel to be the reference level. It's the position with respect to which we measure this height. So, kinetic energy is one half times mass times speed squared and its potential energy up here, is mass times acceleration due to gravity times the height above the reference level. So the height is going to be equal to the radius and -- because when it's down here it's going to be this distance r from the pivot and so that’s the height that it has when it's horizontal. So we can substitute r in place of h and we'll also multiply both sides by 2 and divide both sides by m, then switch the sides around and take the square root of both sides to solve for v. v is going to be the square root of 2 g r. So it's the square root of two times 9.8 meters per second squared, times 14 meters which give 16.6 meters per second. So the centripetal acceleration will be that speed squared divided by the radius of curvature of the path. So that's 16.565 meters per second squared, divided by 14 meters giving 19.6 meters per second squared. This is a free body diagram of the rider and there's the force of the ride applies upwards, we'll call that F n for normal force, and then there's the force of gravity downwards and it's intentional that I've drawn the normal force longer than gravity because this person is going to accelerate upwards. They're moving upwards really quickly at this point here. I mean -- well, I guess that's a bit the wrong way to say it. They're not really moving upwards at this point but they are accelerating upwards and sometime later they will be moving upwards. So they have some centripetal acceleration there and that's due to the fact that this normal force is greater than gravity. So, the centripetal force is the normal force upwards, minus the gravity downwards, and that's going to be mass times centripetal acceleration. We can add force of gravity to both sides. So the centripetal forces is like a net force radially speaking and both of these forces are acting radially. This one is pointing towards the center and this one is pointing away from the center. So now we have normal force is mass times centripetal acceleration plus force due to gravity and substitute m g in for f g and then factor out the common factor m between those two terms and you have the normal force is mass times bracket centripetal acceleration plus gravitational acceleration. So 60 kilograms, mass of the rider, times 19.6 meters per second squared, centripetal acceleration, plus 9.8 meters per second squared, acceleration due to gravity, which gives 1760 newtons. If we compare that to gravity, we can divide the two. So here's the expression for the force due to the ride and divide that by m g and the m's cancel and so this ratio of F n over F g is the same as a c plus g over g. That's 19.6 meters per second squared plus 9.8 divided by 9.8 giving 3. So the normal force is greater than gravity by a factor of three, and that's reasonable because it should be greater since they're accelerating upwards. But it shouldn't be too much greater because that would cause injury.

