Question
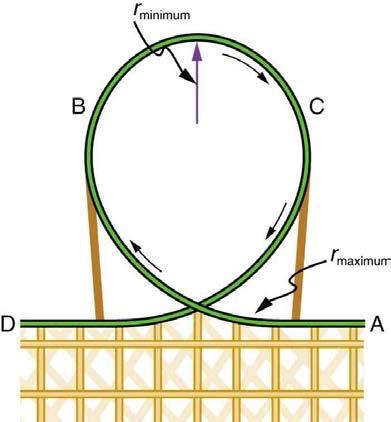
Modern roller coasters have vertical loops like the one shown in Figure 6.38. The radius of curvature is smaller at the top than on the sides so that the downward centripetal acceleration at the top will be greater than the acceleration due to gravity, keeping the passengers pressed firmly into their seats. What is the speed of the roller coaster at the top of the loop if the radius of curvature there is 15.0 m and the downward acceleration of the car is 1.50 g?
<b>Figure 6.38</b> Teardrop-shaped loops are used in the latest roller coasters so that the radius of curvature gradually decreases to a minimum at the top. This means that the centripetal acceleration builds from zero to a maximum at the top and gradually decreases again. A circular loop would cause a jolting change in acceleration at entry, a disadvantage discovered long ago in railroad curve design.
Figure 6.38 Teardrop-shaped loops are used in the latest roller coasters so that the radius of curvature gradually decreases to a minimum at the top. This means that the centripetal acceleration builds from zero to a maximum at the top and gradually decreases again. A circular loop would cause a jolting change in acceleration at entry, a disadvantage discovered long ago in railroad curve design.
Question by OpenStax is licensed under CC BY 4.0
Final Answer

14.8 m/s14.8 \textrm{ m/s}

Solution video

OpenStax College Physics for AP® Courses, Chapter 6, Problem 31 (Problems & Exercises)

OpenStax College Physics, Chapter 6, Problem 31 (PE) video thumbnail

In order to watch this solution you need to have a subscription.

Start free trial Log in
vote with a rating of votes with an average rating of .
Chevron left Prev
Next Chevron right

Calculator Screenshots

  • OpenStax College Physics, Chapter 6, Problem 31 (PE) calculator screenshot 1
Video Transcript
This is College physics Answers with Shaun Dychko. We can rearrange the centripetal acceleration formula to solve for v. We multiply both sides by r and switch the sides around and also take the square root of both sides. So we have v equals the square root of the radius of curvature times the centripetal acceleration. So we're told that at the very top of the roller coaster loop, the radius of curvature is 15 meters and the acceleration is 1.5 times g and g is 9.8 meters per second squared. So we have 14.8 meters per second must be the speed at the top of the loop.