Question
Saturn's moon Titan has a radius of m and a
measured gravitational field of . What is its mass?
Final Answer
Solution video
OpenStax College Physics for AP® Courses, Chapter 6, Problem 4 (Test Prep for AP® Courses)

vote with a rating of
votes with an average rating of
.
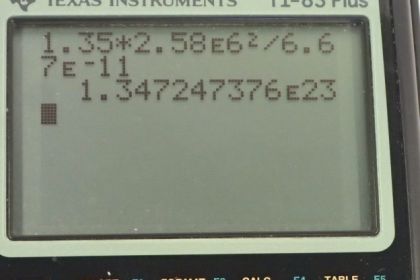
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. To calculate the mass of Saturn's moon Titan based on knowing the acceleration due to gravity there and the radius of that moon. So Newton's second law says that the mass of some object that's free falling on the moon and that mass is M times the acceleration which is given the special letter G for acceleration due to gravity and subscript T for on Titan. So that mass times acceleration equals the net force on the free falling object of which there's only one and that is the force due to gravity which is the universal gravitational constant times the mass of the moon times the mass of the thing falling divided by the distance between you know, the center of the thing falling and the center of the moon but we'll just take this to be the radius of the moon because it's going to be a small distance off the surface of course. So these M's cancel leaving us with acceleration due to gravity of Titan. It's G times mass of the moon divided by radius of the moon squared. So we can solve for m by multiplying both sides by r squared over G and we get the mass of the moon then is 1.35 meters per second squared times—the moon's radius—2.58 times 10 to the 6 meters squared divided by the gravitational constant which gives 1.35 times 10 to the 23 kilograms is the mass of the moon Titan.