Question
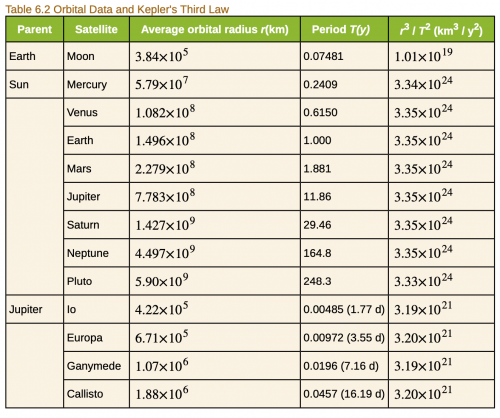
Find the ratio of the mass of Jupiter to that of Earth based on data in Table 6.2.
Final Answer
Solution video
OpenStax College Physics for AP® Courses, Chapter 6, Problem 46 (Problems & Exercises)
vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
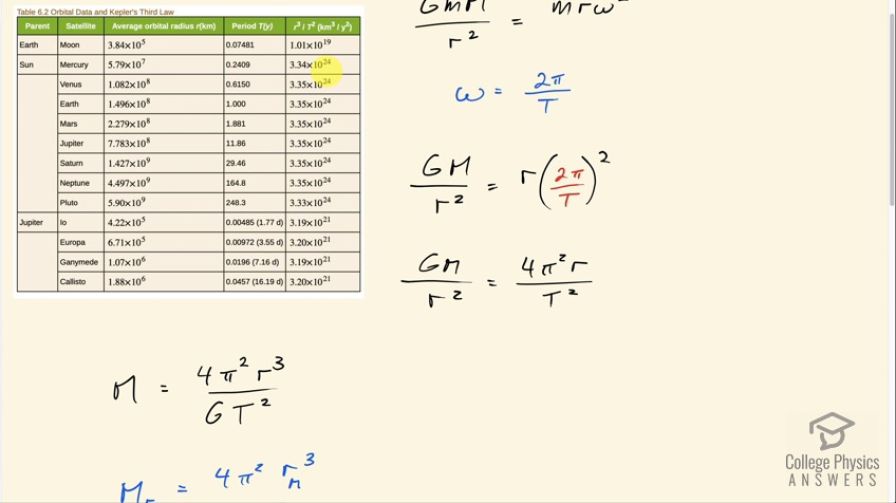
This is College Physics Answers with Shaun Dychko. We are going to calculate the ratio of Jupiter's mass to that of Earth using data in this table [6.2]. So we know that the gravitational force exerted by a central body such as Jupiter or such as Earth equals the centripetal force on the orbiting body, the Moon, in other words. So we'll consider the Io moon for Jupiter and the only moon for Earth and well let's, you know, do a bit of work here to get a r cubed over T squared showing in our work; we are gonna solve for the mass of this central body, in other words so we'll find an expression for the mass of the Earth or Jupiter. So the angular speed of the satellite, the Moon in other words, is the orbit, number of radians in an orbit which is 2π divided by the period of an orbit. And so we substitute that in for ω and so we have universal gravitational constant times the mass of the planet divided by the distance to the orbiting moon squared equals that distance r times 2π over T squared. So we apply this exponent 2 and we get 4π squared times r over T squared on the right side and then we solve for the mass of the planet by multiplying both sides by r squared over G and we get then that the mass of the planet is 4π squaredr cubed over GT squared. So for the Earth, we are plugging in the Earth-Moon distance cubed or divided by the Moon orbital period squared and for Jupiter, it's all the same factors except for the distance to one of the moons— let's take Io for example—cubed divided by the period of Io's orbit squared. So then when we divide these two masses— divide the mass of Jupiter by the mass of Earth— and we have this expression for the mass of Jupiter divided by this expression for the mass of Earth but dividing a fraction by a fraction is messy so I'm going to instead multiply by the reciprocal of the denominator. So we are gonna multiply by the reciprocal of the mass of the Earth which is G times period of the Moon squared over 4π squared Earth-Moon distance cubed. And we see that the 4π squared G's cancel and this second fraction, let's flip it over and make it to exponent negative 1 which in the end doesn't change it which is good so we can multiply by this thing flipped over to the power of negative one because this number is what's given to us in this data table. So we have 3.19 times 10 to the 21 which is r cubed over T squared for the Jupiter's moon Io and multiplied by 1.01 times 10 to the 19 to the power of negative 1. And, you know, if you don't like this negative 1 business, you could have also written this as r cubed for Io over period of Io squared divided by distance between the Earth and the Moon divided by the period of the Moon squared; this would be fine and you would get the same answer I just don't like having fractions within fractions. So we end up with 316 so Jupiter's mass is greater than Earth's by a factor of 316.
