a)
b)
Solution video
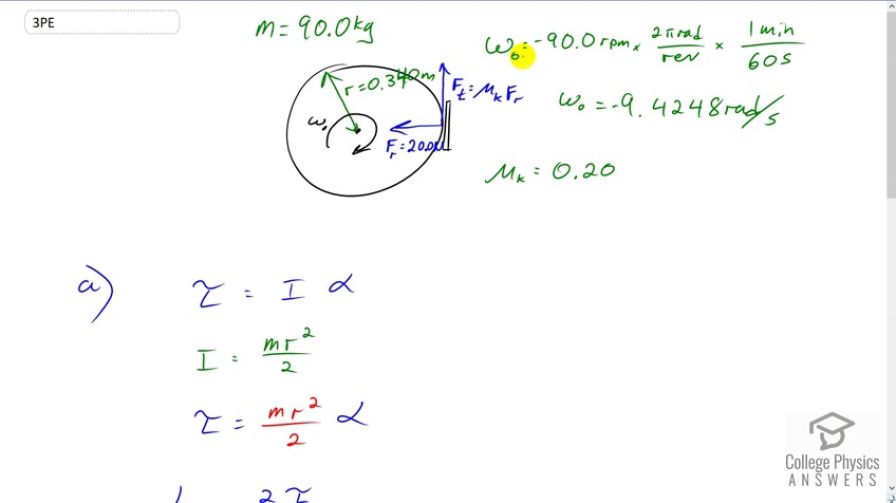
OpenStax College Physics, Chapter 10, Problem 3 (Problems & Exercises)
Calculator Screenshots
Comments
Hey Shaun, just wondering if your answer for part a should be negative because torque is negative when it is slowing something thus your angular velocity would be -0.26 rad/s^2. Thanks in advance for your help!
Hi John, thank you for the question. I mention the sign of part (a) at 3:35 in the video. The sign depends on how you've set up your coordinate system - it could alternatively be set up with part (a) negative, as you suggest, but then part (b) would need to be positive. In the coordinate system I've chose, which follows the textbook's convention, counterclockwise is positive whereas clockwise is negative. It's a misconception to think "negative torque slows things down" - consider the linear case which is easier to picture: an object moving in the negative direction experiencing a net force also in the negative direction will speed up. The sign strictly refers to direction - not "speeding up or slowing down". The ccw torque is positive (part (a)) since ccw is the positive direction in the conventional coordinate system, whereas the number of turns before stopping is negative (part (b)) since it's turning cw.
Hope this helps,
Shaun



