Question
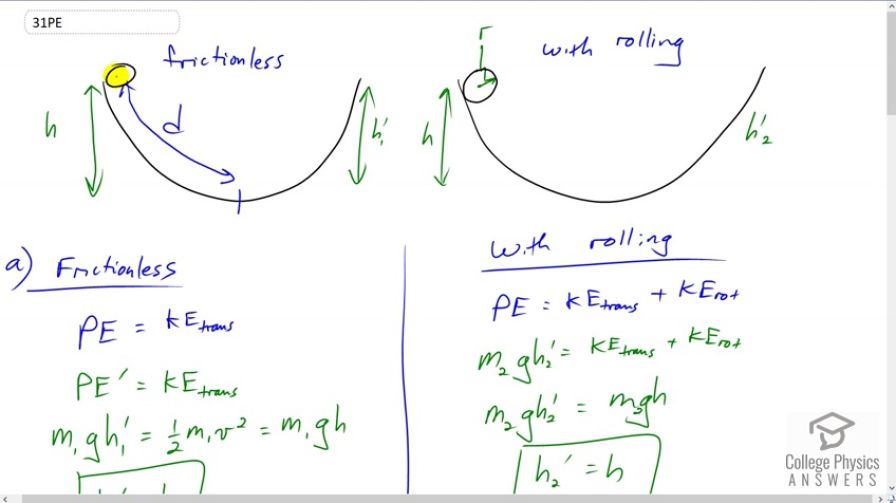
Consider two cylinders that start down identical inclines from rest except that one is frictionless. Thus one cylinder rolls without slipping, while the other slides frictionlessly without rolling. They both travel a short distance at the bottom and then start up another incline. (a) Show that they both reach the same height on the other incline, and that this height is equal to their original height. (b) Find the ratio of the time the rolling cylinder takes to reach the height on the second incline to the time the sliding cylinder takes to reach the height on the second incline. (c) Explain why the time for the rolling motion is greater than that for the sliding motion.
Final Answer
a) see solution video
b)
c) Translational velocity for the rolling case is smaller since some energy is allocated to rotational kinetic energy. A smaller translational velocity means a greater time taken.
Solution video
OpenStax College Physics, Chapter 10, Problem 31 (Problems & Exercises)
vote with a rating of
votes with an average rating of
.
Video Transcript
This is College Physics Answers with Shaun Dychko. On the left side here we have a picture where the cylinder is going down this slope but it's a frictionless slope and so it does not roll. Over here it is rolling. Now in the frictionless case let's figure out what final height it will reach. We'll call that h one prime, the one labels the frictionless situation and the prime means after it goes up the next side of the incline. So the potential energy at the very beginning is going to equal the kinetic energy that's translational at the bottom of the incline, and the potential energy at the very end when it goes back up the other side we'll call that p e prime, is going to equal this kinetic energy translational at the bottom. So since both of these things equal this same translational kinetic energy, that means they equal each other and so m one g h one prime which is the potential energy on the other side, equals m one g h which is the initial potential energy. The m one and g's cancel and we find that h one prime is equal to h. So it reaches the same height on the other side as it started in other words. Now when there is rolling, it really doesn't change anything. The initial potential energy gets turned into translational kinetic energy just the same as it did before in the frictionless case but then there is also this rotational kinetic energy term added as well. But nevertheless the potential energy after it goes up the other side, also equals that same total kinetic energy and so we can say that the two potential energies before and after are also the same. So again h two prime equals the same initial height. Okay. Now the more interesting question is finding the ratio of the times that it takes for the cylinder to reach its maximum height on the other side because the times are not the same. So in the frictionless case we'll figure out the time it takes and we're going to only just to make things a bit simpler, we'll figure out the time it takes to go down one incline and never mind the time it takes to go up the other side because if we take a ratio of half the time in each case, that will be the same result as taking the ratio of the full time in each case. Okay. So we have the distance that it travels which is the distance along this curve, distance d, is going to equal the average velocity multiplied by time. The time's going to be d divided by average velocity. It has no initial velocity to begin with and so this works out to two d over v one f. This is the final speed in the first case where there is no friction. So let's figure out what that's going to be. The translational kinetic energy it has at the bottom of the incline will equal the gravitational potential energy it has at the beginning and when we solve this for v f, it's going to be square root two g h. So we'll substitute that in for v one f here, so that means t one equals two d over square root two g h which in simplified form is d times square root two over g h. Okay. So that's the time in the first case. Then in the second case with rolling, we have t two is two times d over v two f just as we did over here. But there is going to be a different final speed in the second case. So in the second case, the final kinetic energy at the bottom of the incline is going to be one half m two v two f squared. But there is also going to be this one half times moment of inertia times angular velocity squared. Those two together are going to total the initial gravitational potential energy. So for a cylinder the moment of inertia will be its mass times its radius squared over two, and we'll also make a substitution for angular velocity and write it as translational velocity divided by its radius. Then substitute for each of those things, i and omega here. The m's cancel everywhere and so we end up with v fsquared over two, and on this term here we have an r squared in the denominator and an r squared in the numerator so the r squareds cancel and we're left with v f squared over four equals g h. This works out to three v f squared over four. Multiply top and bottom by two here, and then to make a common denominator and then add numerators, two and one makes three there. Then v f squared -- well, actually v f I should say, is going to equal four g h over three square rooted. In simplified form that's two times square root of g h over three. Now we substitute that in for the final velocity here and instead of dividing by it I'm going to multiply by its reciprocal. So I'm multiplying by one half times square root three over g h. The one halfs cancel, we're left with d times square root of three over g h. So that's time two. Then we take the ratio of those times t two over t one. We get d times square root three over g h and then multiply by the reciprocal of t one say. So we're going to multiply by one over d times square root g hover two. That's what I did here and the square root g h's cancel and the d's cancel leaving us with square root three over two is the ratio of the times. This is a number that is greater than one and it means that time two is greater that time one. That makes sense because in the rolling case the translational velocity is smaller and this time depends entirely on the translational velocity. In the rolling case the translational velocity will be smaller because some of the kinetic energy is being allocated to rotational kinetic energy. That means that translational kinetic energy will be smaller than it was with no rolling. The smaller translational velocity is going to take longer to reach the top of the other incline.