Question
(a) Calculate the angular momentum of an ice skater spinning at 6.00 rev/s given his moment of inertia is 0.400 kg⋅m20.400 \textrm{ kg} \cdot \textrm{m}^2. (b) He reduces his rate of spin (his angular velocity) by extending his arms and increasing his moment of inertia. Find the value of his moment of inertia if his angular velocity decreases to 1.25 rev/s. (c) Suppose instead he keeps his arms in and allows friction of the ice to slow him to 3.00 rev/s. What average torque was exerted if this takes 15.0 s?
Question by OpenStax is licensed under CC BY 4.0
Final Answer

a) 15.1 kg⋅m2s15.1 \textrm{ kg} \cdot \textrm{m}^2 \textrm{s}

b) 1.92 kg⋅m21.92 \textrm{ kg}\cdot \textrm{m}^2

c) −0.503 kg⋅m2/s2-0.503 \textrm{ kg} \cdot \textrm{m}^2 \textrm{/s}^2

Solution video

OpenStax College Physics, Chapter 10, Problem 41 (Problems & Exercises)

OpenStax College Physics, Chapter 10, Problem 41 (PE) video thumbnail

In order to watch this solution you need to have a subscription.

Start free trial Log in
vote with a rating of votes with an average rating of .
Chevron left Prev
Select problem
Next Chevron right

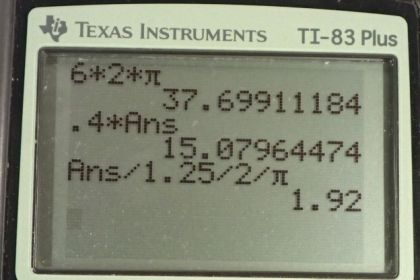
Calculator Screenshots

  • OpenStax College Physics, Chapter 10, Problem 41 (PE) calculator screenshot 1
  • OpenStax College Physics, Chapter 10, Problem 41 (PE) calculator screenshot 2
Video Transcript
This is College Physics Answers with Shaun Dychko. We’re given the moment of inertia of an ice-skater and his initial angular velocity. We convert that six revolutions per second into radians per second by multiplying by 2 pi radians per revolution, leaving us with radians per second, that is 37.699 radians per second. Part a asks us to find the angular momentum of the skater, and so we multiply the moment of inertia by the angular velocity, so that’s 0.4 kilograms-meters squared times 37.699 radians per second, and we get 15.1 kilograms-meters squared per second. Now if they extend their arms, their moment of inertia will increase because they are moving some of their mass further away from the axis of rotation, from the centre of the body, and that’s going to increase their moment of inertia and we have to calculate what the new moment of inertia is. The angular momentum isn’t going to change, that’s going to be… And we divide that by the new angular velocity that we’re told is one and a quarter revolutions per second, so we multiply that one and a quarter by 2 pi radians for every revolutions and we divide that into 15.0796 kilograms-meters squared per second that we calculated in part a and we get 1.92 kilograms-meters squared. Part c says supposed that they keep their arms by their sides so the moment of inertia does not change, and so it is still 0.4 that we were given to begin with. Supposed that the friction due to the ice as they twirl around is causing them to slow down and they have some final angular velocity of three revolutions per second which we convert into radians per second, and then it takes this amount of time for that change to occur, what will be the torque that the ice is applying on the skater. So torque is moment of inertia multiplied by angular acceleration, so we find the difference in the angular velocity divided by the time and then substitute that in for alpha, multiplied by the moment of inertia to get our torque. So we have three revolutions per second times 2 pi radians per revolution minus the initial angular velocity of 37.699 radians per second, and divide that by 15 seconds, and we get negative 1.2566 radians per second squared. Multiply that by the moment of inertia 0.4, and we get negative 0.503 kilograms-meters squared per second squared is the torque, and this torque is negative because it is opposing the initially positive angular velocity.