Question
Repeat Example 10.15 in which the stick is free to have translational motion as well as rotational motion.
Example 10.15
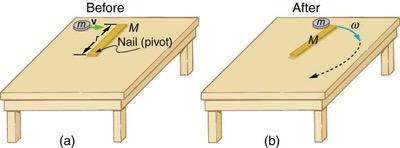
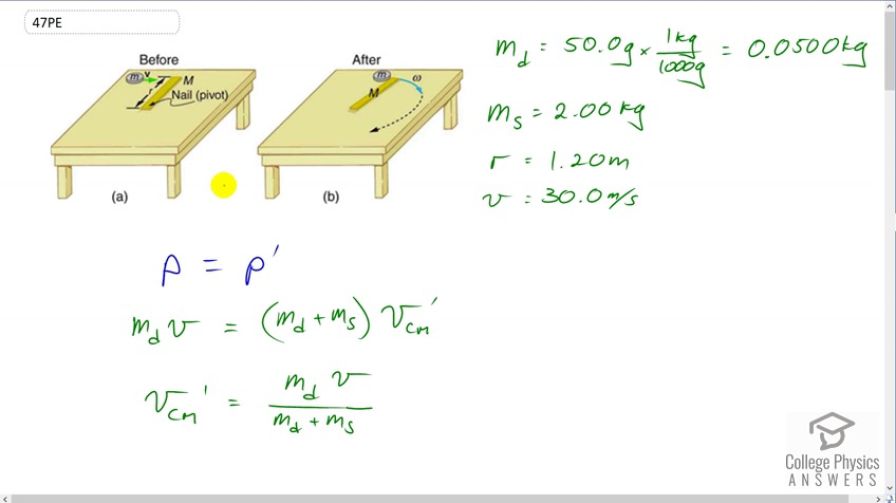
Suppose the disk in Figure 10.26 has a mass of 50.0 g and an initial velocity of 30.0 m/s when it strikes the stick that is 1.20 m long and 2.00 kg.- What is the angular velocity of the two after the collision?
- What is the kinetic energy before and after the collision?
- What is the total linear momentum before and after the collision?
Final Answer
a)
b)
c)
Solution video
OpenStax College Physics, Chapter 10, Problem 47 (Problems & Exercises)
vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. In problem 47 here, we’re repeating example 10.15 but with the change being that we no longer have a nail here to create a pivot at this point. That still will be the pivot but this point is free to also translate to the side and that’s going to create some complication in our work here and we’ll see how to deal with that in a second. I begin by writing down information that were given and we have the disc hitting the end of the stick, if you’ve watched the solution to number 43, we have the disc hitting the stick here at a position of 0.1 meters from the pivot, but this question, this drawing is accurate with the disc hitting the end of the stick, the only change this drawing being that there is no nail here at the pivot anymore. So, we need to know what the velocity of the center of mass of the system will be after the disc sticks to the stick. And so we solve for that first and we’ll say that the momentum before the disc hits the stick is the same as the momentum after it collides. So we have momentum before is just mass of the disc multiplied by its velocity because the stick is not moving. And then afterwards we have the mass of the two things combined multiplied by the velocity of the center of mass of the disc-stick system. And we’ll solve for vcm prime by dividing both sides by the total mass of the system disc plus stick, so vcm prime is mass of the disc times v divided by md plus ms. Okay. So, that’s just a bit of preamble. So we’re gonna solve this by saying the angular momentum of the system before the collision is the same as the angular momentum after the collision. And the, now well, when I say before collision, I don’t really mean before the collision, I just mean before it’s rotating. And so there is just this instant of time when the collision has happened but the stick hasn’t started moving yet, which you could also say is before the collision, but anyway so it’s that instant that we consider to begin with, that’s what L represents. L prime is the case where the disc has stuck to the stick and they are rotating together and we’ll have an expression for that too, and then we’ll equate the two expressions to solve for omega prime. So before rotating, we have the angular momentum is going to be the moment of inertia of the system which is just that of the disc because the stick hasn’t started rotating yet so it’s not part of this rotating system. The system consists only of the disc more-or-less here. And then we multiply that by the angular velocity but the angular velocity is going to be the initial velocity of the disc minus the velocity of the center of mass of the system, so the disc has collided with the stick and the two are sort of moving to the right here but the stick hasn’t started rotating yet and another way to think of this is, we’re looking for the velocity of the disc in the reference frame of the center of mass of the system, or the velocity of the disc with respect to the center of mass, and so that’s why we have to calculate this center of mass of the system up here. So we substitute in for the vcm prime and we replaced it with md v over md plus ms, we also have one of the rs cancel here and so we just have md times r to the power of one. And then I made a common denominator by multiplying this by md plus ms and also factor out the v, and so when you factor out the v this becomes the number one, so we multiply by md plus ms, it just becomes md plus ms and then minus this md, all divided by the common denominator, and md minus md makes zero there and we’re left with just ms inside the bracket. So we have md ms times rv, all over md plus ms. So that’s the angular momentum after the collision but before rotating. And then after rotating, we have a new moment of inertia, which will be that of the disc as we have before plus the moment of inertia of the stick, which has a formula mass times radius squared divided by three when you have a stick rotating about an axis at one end. Then we multiply that by omega prime, and that’s the angular momentum after collision and after rotating. What else did I do here. Factor out the r squared and the omega prime, also make a common denominator of three inside the bracket so that’s why you have the number three multiplied by md, and so this whole thing is over three but I wrote the three outside the bracket here, so we have r squared omega prime over three times 3 md plus ms. So these two things are equal to each other so let’s substitute in these two expressions we just created and we have this one here for L, md ms r v over md plus ms equals this expression here for L prime, r squared omega prime over three times 3 md plus ms. And then we solve for omega prime. We multiply by three over r squared 3 md plus ms, we do that to both sides. And we get omega prime is three times the product of the masses times the initial velocity of the disc divided by the length of the stick multiplied by the sum of the two masses multiplied by three times the mass of the disc plus the mass of the stick. And we end up with three times 0.05 kilograms times two kilograms times 30 meters per second over 1.2 meters times 0.05 kilograms plus two times by three times 0.05 kilograms plus two, and you get 1.70 radians per second. Alright. Now the kinetic energies, we have before collision is straight forward, it’s one half mass of the disc times its linear velocity squared, and we get 22 and a half Joules. And then after the collision, we have a term representing the translational kinetic energy, one half mass of the system multiplied by the velocity of the center of mass of the system squared, plus the rotational kinetic energy. And the velocity of the center of mass, we have a formula we found before, and so we’ll plug in some numbers to get a value for it. So 0.05 kilograms times 30 meters per second divided by the total mass, giving us 0.73171 meters per second. And the moment of inertia of the system after it rotates is the moment of inertia of the disc plus that of the stick, and this gives us 1.2 meters squared multiplied by 0.05 kilograms plus two kilograms over three, which is 1.032 kilograms-meters per second squared, oh sorry kilograms-meters squared I should say. And then we plug in numbers into our KE prime formula, so we have one half times the total mass multiplied by the velocity of the center of mass and then add to that one half times the moment of inertia multiplied by the angular velocity which we calculated in part a and we square that, and that equals 2.04 Joules. And then the momentum is going to be the same before and after collision, and so let’s just calculate it from before the collision, that’s 0.05 kilograms times 30 meters per second which is 1.50 kilograms-meters per second.


