Question
A gymnast doing a forward flip lands on the mat and exerts a 500-N · m torque to slow and then reverse her angular velocity. Her initial angular velocity is 10.0 rad/s, and her moment of inertia is .(a) What time is required for her to exactly stop her spin? (b) What is unreasonable about the result? (c) Which premises are unreasonable or inconsistent?
Final Answer
a) 2ms
b) 2ms is too short
c) The moment of inertia is too small.
Solution video
OpenStax College Physics, Chapter 10, Problem 19 (Problems & Exercises)
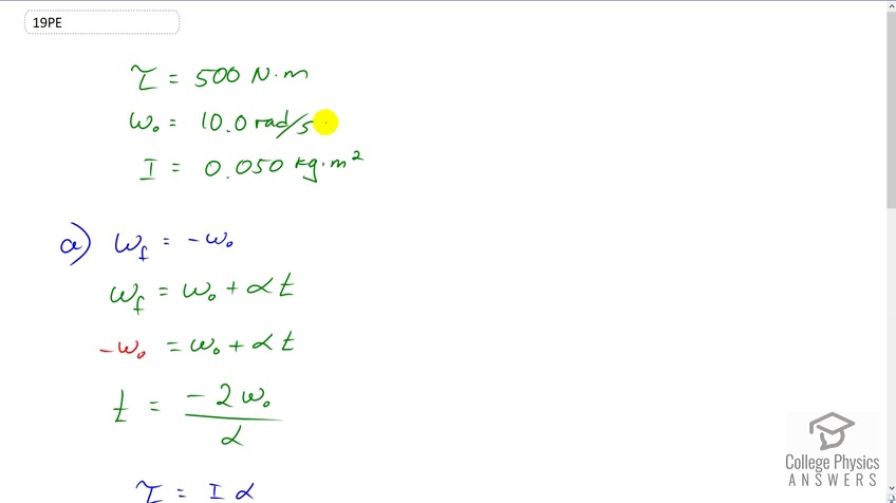
vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. A gymnast exerts a torque of 500 Newton meters when she lands and her initial angular velocity is 10 meters per second and her final angular velocity is going to be the negative of that because exactly is reversed. Her moment of inertia we're told is 0.05 kilogram meter squared. So the final angular velocity is going to be the initial plus angular acceleration times time, and we can substitute negative w or omega naught in place of omega f and then solve for t. We'll subtract omega naught from both sides and then divide both sides by alpha and we get this expression for t. This is useful because we can figure out what alpha is based on the information given. Given the torque and given the moment of inertia we can find alpha because torque is moment of inertia multiplied by alpha. So divide both sides by i and we get alpha is torque divided by moment of inertia and so we can substitute that in up here. Instead of substituting tau over i in the denominator, I'm multiplying by its reciprocal just because I don't like to have fractions within fractions, so multiplying by i over tau. So the time is negative two times 10 radians per second multiplied by 0.05 kilogram meters squared, divided by negative 500 Newton meters and I gave the torque a negative sign because it should be in the opposite direction to the initially positive angular velocity, noted to be reversing that. So this works out to positive 0.002 seconds which is two milliseconds. That is unrealistically short period of time. Nobody is going to do this is two milliseconds. The moment of inertia is way too small. If we model the gymnast as a cylinder of mass 50 kilograms say, and a radius of 0.3 meters, their moment of inertia would be about 15 kilogram meter squared which is three orders of magnitude bigger than the value given of 0.05.
