Question
Repeat Example 10.15 in which the disk strikes and adheres to the stick 0.100 m from the nail.
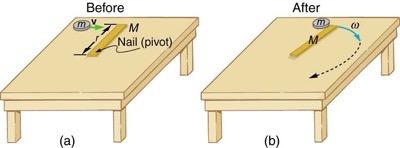
Example 10.15
Suppose the disk in Figure 10.26 has a mass of 50.0 g and an initial velocity of 30.0 m/s when it strikes the stick that is 1.20 m long and 2.00 kg.- What is the angular velocity of the two after the collision?
- What is the kinetic energy before and after the collision?
- What is the total linear momentum before and after the collision?
Final Answer
a)
b) ,
c) ,
Solution video
OpenStax College Physics, Chapter 10, Problem 43 (Problems & Exercises)

vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. We’re going to answer example 10.15 again in question 43 here, but the difference will be that this picture is not quite accurate, I just copied it from the example but it’s meant to have the disc hitting the stick at this location here which is 0.1 meters away from the pivot point where the nail is holding this end of the stick to the table. So we could have a distance here rd for disc is 0.1 meters, and the disc is going to stick to the stick and then they will rotate together as a single object. So the mass of the disc is 50 grams which we converted to kilograms, and the mass of the stick is two kilograms, and the length of the stick is 1.2 meters, and the radius of the curvature for the disc will be 0.1 meters because that’s where it strikes the stick, is 0.1 meters away from the pivot, and it has an initial velocity of 30 meters per second as it’s sliding on this frictionless table. Now angular momentum will be conserved and so this represents the angular momentum at the very instant before the stick begins to move, and at that instant when the disc is just beginning to contact the stick, the angular, we can speak about an angular momentum and that will be that of just the disc because the stick hasn’t started moving yet and we’ll take the angular moment of inertia to be that of a point mass with the disc at a distance r subscript d for disc away from the pivot. And we’ll think about an angular velocity for the disc to be its translational velocity v 30 meters per second divided by rd its distance from the pivot. And then after the stick begins to move, we have a new moment of inertia which is that of the disc and the stick added together, and the stick will be modelled as a rod rotating about an axis of rotation at one end which has a formula mass times length squared over three, and then multiply that by the angular velocity after the collision. So omega prime is the first thing we’re going to solve for, we divide both sides by I prime to solve for it. Then, we’re going to figure out the kinetic energy of the system before and after collision and also the linear momentum before and after collision. So after the collision, we have this total moment of inertia equaled to that of the disc plus the moment of inertia of the stick. So we have written here the result of doing this, we have the angular velocity after the disc is stuck to the stick and they both start to move equals the initial angular momentum divided by the final moment of inertia. And so we make substitutions here now and we have the initial moment of inertia is mass of the disc times radius of the disc squared, I mean not the radius of the disc itself but radius of its curve path, multiplied by its angular velocity which is its linear velocity divided by rd and then we divide it by the total moment of inertia which we copied from here, and one of the rds cancelled here so we’re just left with md rd v on the top. Then we plug in numbers and we have 0.05 kilograms mass of the disc times 0.1 meters away from the pivot multiplied by 30 meters per second, and divide that by 0.05 kilograms times 0.1 meters squared plus two kilograms times 1.2 meters squared divided by three, that 1.2 meters being the length of the stick, and we have 0.156 radians per second will be the angular velocity after the disc sticks to the stick. The kinetic energy before collision is straight forward, it’s one half times mass of the disc times the velocity of the disc initially squared, so that’s one half times 0.05 kilograms times 30 meters per second squared, giving us 22 and a half Joules. And the kinetic energy after collision will be entirely rotational, and so it’s going to be one half moment of inertia after collision multiplied by the angular velocity after collision squared. The reason there is no one half mv squared term here is because there’s no linear translation of the center of mass of the system, so it’s not moving anywhere, it’s only rotating so it’s just rotational kinetic energy. Okay. So KE prime is going to be one half times the moment of inertia, and we have the formula already that we discussed, multiplied by omega prime that we calculated in part a. And so we plug in numbers to get our answer. So one half times 0.05 kilograms times 0.1 meters squared plus two kilograms times 1.2 meters squared over three times 0.15617 radians per second squared, giving us 0.0117 Joules is the kinetic energy after the collision. The momentum before collision is mass of the disc multiplied by its initial speed, 0.05 kilograms times 30 meters per second, giving us 1.5 kilograms-meters per second. After the collision, we have the disc moving at a certain speed and we have the center of mass of the stick also moving, and we’ll add those two momentum together to get the total momentum after collision. So the velocity of the disc is going to be its angular velocity multiplied by its distance from the pivot, and the velocity of the stick’s center of mass is going to be the angular velocity after collision multiplied by the position of the center of mass. Now since the stick has its mass distributed uniformly along its length, its center of mass will be located at the halfway point, it will be at its geometric center. And so we have omega prime times length of the stick rs over two. So we substitute each of those into this momentum formula here, we’re replacing vd prime with this and replacing vscm prime with this, and we can factor out the omega prime common factor and then plug in numbers, we have 0.15617 radians per second that we calculated in part a, multiplied by 0.05 kilograms times 0.1 meters plus two kilograms times 1.2 meters over two, giving us 0.188 kilograms-meters per second is the momentum.



