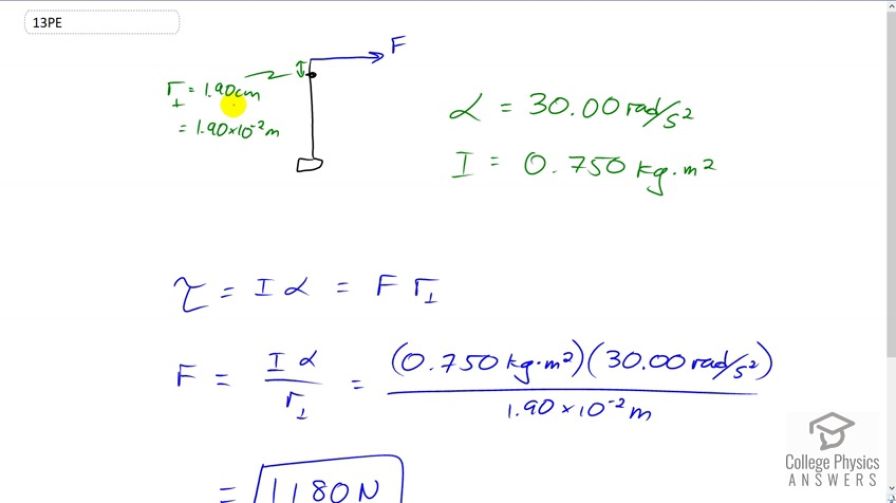
Question
A soccer player extends her lower leg in a kicking motion by exerting a force with the muscle above the knee in the front of her leg. She produces an angular acceleration of and her lower leg has a moment of inertia of . What is the force exerted by the muscle if its effective perpendicular lever arm is 1.90 cm?
Final Answer
Solution video
OpenStax College Physics, Chapter 10, Problem 13 (Problems & Exercises)
vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. This black dot here represents the pivot point that is the knee and the upper leg muscle has a lever arm of 1.9 centimeters which we write as 1.90 times ten to the minus two meters. It's going to be exerting a torque in other words about this pivot point, and it's going to cause an angular acceleration of the lower leg of 30 radians per second squared. We're given the moment of inertia of the lower leg as well. It's 0.75 kilogram meter squared. So the question is what is this force being exerted by the muscle? Well, torque is moment of inertia multiplied by acceleration. This is the Newton's Second Law in a rotational context and torque is also force multiplied by perpendicular lever arm. So we can divide both sides by the lever arm here and solve for the force F. So the force is moment of inertia times alpha divided by r. So that's 0.75 kilogram meter squared times 30 radians per second squared, divided by 1.9 times ten to the minus two meters, giving us 1180 newtons.
