Question
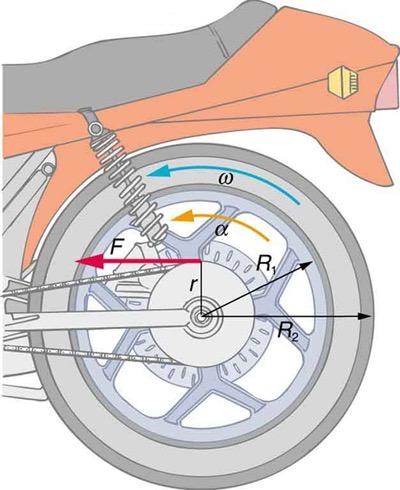
Consider the 12.0 kg motorcycle wheel shown in Figure 10.38. Assume it to be approximately an annular ring with an inner radius of 0.280 m and an outer radius of 0.330 m. The motorcycle is on its center stand, so that the wheel can spin freely. (a) If the drive chain exerts a force of 2200 N at a radius of 5.00 cm, what is the angular acceleration of the wheel? (b) What is the tangential acceleration of a point on the outer edge of the tire? (c) How long, starting from rest, does it take to reach an angular velocity of 80.0 rad/s?
Final Answer
a)
b)
c)
Solution video
OpenStax College Physics, Chapter 10, Problem 15 (Problems & Exercises)

vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. We have a motorcycle wheel which we're going to model as an annular ring. An annular ring is a ring that has a significant thickness. So there is an inner radius r one and an outer radiusr two, and we're given what those radii are here. The mass is 12 kilograms. There is a force applied by the chain, 2200 newtons, and that's exerted at a distance of 5 centimeters from the axle which is five times ten to the minus two meters. In part A, we're asked to figure out what is the angular acceleration of the wheel? So we know the torque applied by this chain force equals the moment of inertia of the wheel multiplied by its angular acceleration. The moment of inertia when we look it up in the textbook for an annular ring, it's the mass of the ring divided by two times the sum of the squares of the inner and outer radii. So we can substitute that in for i and then also say that this torque is the force multiplied by the radius and we assume that these are perpendicular, and so we can solve for alpha by dividing by this stuff and then multiplying by two. So we're going to go two over m times r one squared plus r two squared. We do that on both sides of this equation. So we're left with alpha on its own equals two times the force applied multiplied by the chain radius, divided by the total mass of the wheel, multiplied by r one squared plus r two squared. So we have two times 2200 newtons times five times ten to the minus two meters, divided by 12 kilograms times 0.28 meters squared, plus the outer radius of 0.33 meters squared. That gives 97.9 radians per second squared. Then the tangential acceleration of a point on the outside of the wheel is going to equal the outer radius multiplied by the angular acceleration which is alpha, not omega, there. So that's 0.33 meters times the answer from part A which is 97.882 radians per second squared, and this gives 32.3 meters per second squared. Then in part C, we're asked to figure out how long will it take for the wheel to reach an angular velocity of 80 radians per second? So we have the final angular velocity is the initial angular velocity plus the angular acceleration multiplied by time. We can solve for t by subtracting omega naught from both sides and then dividing both sides by alpha. So we have t is omega final minus omega naught divided by alpha and so that's 80 radians per second minus an initial angular velocity of zero, divided by the angular acceleration that we calculated in part A of 97.882 radians per second squared. It will take a time of 0.817 seconds to reach 80 radians per second.


