Question
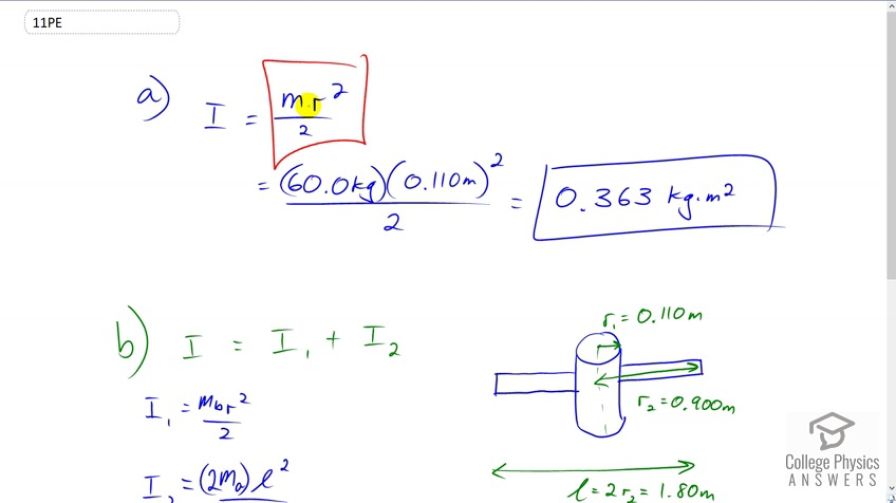
Calculate the moment of inertia of a skater given the following information. (a) The 60.0-kg skater is approximated as a cylinder that has a 0.110-m radius. (b) The skater with arms extended is approximately a cylinder that is 52.5 kg, has a 0.110-m radius, and has two 0.900-m-long arms which are 3.75 kg each and extend straight out from the cylinder like rods rotated about their ends.
Final Answer
a)
b)
Solution video
OpenStax College Physics, Chapter 10, Problem 11 (Problems & Exercises)
vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. The moment of inertia of the skater when her arms are by her side is modeled as a cylinder, and the formula for that is total mass times radius of the cylinder squared divided by two. We had to look up that formula in that table given to us in figure ten dot twelve. So that's 60 kilograms mass times 0.11 meters radius squared divided by two which is 0.363 kilogram meters squared. Then in part two we're told that she extends her arms to the side and so here's the new picture where there is still her cylindrical body in the middle, but it now has a mass of only 52.5 kilograms instead of 60. The rest of the mass is in her arms which are extended 0.9 meters from the center of her body. The total moment of inertia will be the moment of inertia of the cylinder plus the moment of inertia of the two outstretched arms. We can add these together because remember that moment of inertia is the rotational analog to mass when we're talking about linear situations. So in the same way that if you had two blocks stacked on top of each other, you could add their mass together, likewise, when you're talking about a rotational situation you can add together moments of inertia in the same way because they are analogous to each other, mass and moment of inertia. Okay. So well the cylindrical part, her body in the middle, that part is straightforward, it's the same formula as before, the mass of her body times its radius squared divided by two. Now for the arms, the question suggests to model each arm as a rod which is rotating about an axis at the end. But just for fun, I decided to do it a little bit differently and say that let's assume that it's one really long rod with an axis of rotation in the center. The formula for that is the total mass of the rod multiplied by its length squared divided by 12. It works out to the same answer either way. So, we have 52 and a half kilograms times 0.11 meters squared divided by two is the moment of inertia of the body plus the total mass of both arms, two times three and three quarters kilograms, times the total length which is 1.8 meters, and you square that, divide by 12 because that's what the formula says, and you end up with 2.34 kilogram meter squared is the moment of inertia. So you can see that the moment of inertia of the skater changes dramatically just by extending her arms. It goes from 0.363 kilogram meter squared when the arms are beside her body to 2.34 kilogram meter squared when the arms are extended. This is why if she initially had her arms low, and then extended them while she was rotating around, she would slow her angular velocity dramatically because she wouldn't have a larger moment of inertia.
