Question
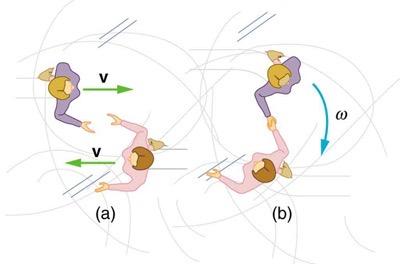
Twin skaters approach one another as shown in Figure 10.39 and lock hands. (a) Calculate their final angular velocity, given each had an initial speed of 2.50 m/s relative to the ice. Each has a mass of 70.0 kg, and each has a center of mass located 0.800 m from their locked hands. You may approximate their moments of inertia to be that of point masses at this radius. (b) Compare the initial kinetic energy and final kinetic energy.
Final Answer
a)
b)
The kinetic energy is the same before and after they join hands.
Solution video
OpenStax College Physics, Chapter 10, Problem 45 (Problems & Exercises)

vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. We have two identical skaters approaching each other, each with a speed of two and a half meters per second, each with a mass of 70 kilograms and each a distance of 0.8 meters away from the axis of rotation which is at the position of their hands. At the instant before they lock hands, they have some angular momentum and that’s going to be the same as the angular momentum after their hands are locked together. Just before their hands are locked together, they are going to have a momentum equaled to two times, because there’s two of them, the moment of inertia of one of them multiplied by the angular velocity of one of them. And this is, I mean, you know, before they locked hands you might say well there is no angular velocity because they are going in a straight line and that’s kind of true but we can imagine that this is just the nanosecond instant before they lock hands and we can think of them as having an angular velocity because they are about to go in a circle. So, we’re told that we can model each skater as a point mass, and so the moment of inertia is going to be mass of the skater times distance from the axis of rotation squared, and the angular velocity will be the translational velocity divided by the radius of their curve path. So we can cancel one of the rs there and we end up with 2mvr is the angular momentum. Now the angular momentum after they lock hands is the moment of inertia multiplied by the new angular velocity and we’ll divide both sides by I prime here and we get omega prime is L prime over I prime, L prime is 2mvr as we talked about up here and we divide that by two times the moment of inertia which is mr squared and this gives v over r in the end, because the twos cancel, the ms cancel and one of the rs cancel, and we’re left with two and a half meters per second divided by 0.8 meters which is 3.13 radians per second. And then we’re meant to find the kinetic energy of the system before and after they lock hands. Before they lock hands, the kinetic energy is entirely translational and so we have one half mv squared as the kinetic energy of each skater and there are two of them so we multiply by two, this works out to mv squared, so 70 kilograms times two and a half meters per second squared, giving us 438 Joules. After they lock hands, the kinetic energy will be entirely rotational, so that’s going to be one half times moment of inertia times angular velocity squared, so that’s one half times 2mr squared because each has a moment of inertia mr squared and there are two of them so multiply by two, and then multiply by omega prime that we found before, square that, and the two cancels with the one half and we’re left with mr squared omega prime squared, so 70 kilograms times 0.8 meters squared times 3.125 radians per second that we calculated before, square that and we get 438 Joules. This shows that the kinetic energy is the same before and after they locked hands.
