Question
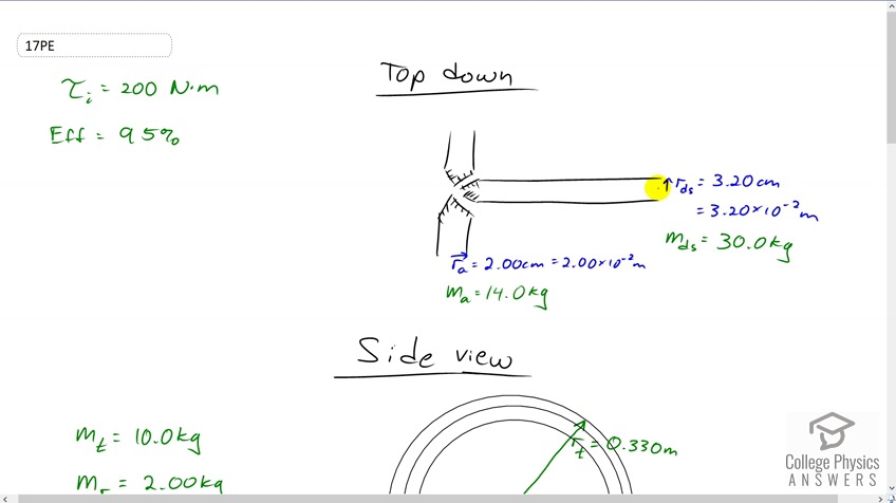
An automobile engine can produce 200 N · m of torque. Calculate the angular acceleration produced if 95.0% of this torque is applied to the drive shaft, axle, and rear wheels of a car, given the following information. The car is suspended so that the wheels can turn freely. Each wheel acts like a 15.0 kg disk that has a 0.180 m radius. The walls of each tire act like a 2.00-kg annular ring that has inside radius of 0.180 m and outside radius of 0.320 m. The tread of each tire acts like a 10.0-kg hoop of radius 0.330 m. The 14.0-kg axle acts like a rod that has a 2.00-cm radius. The 30.0-kg drive shaft acts like a rod that has a 3.20-cm radius.
Final Answer
Solution video
OpenStax College Physics, Chapter 10, Problem 17 (Problems & Exercises)
vote with a rating of
votes with an average rating of
.
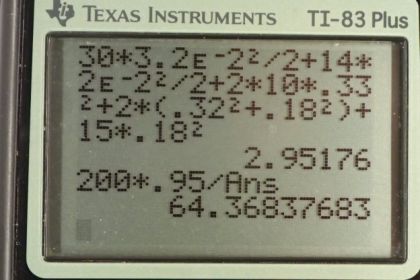
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. When the engine of an automobile 200 Newton meters of torque to the drive train, there are a lot of components involved in the drive train which affect what the angular acceleration will be of the wheel. The engine has to spin the drive shaft and it also has to spin the axles connecting the drive shaft to the wheels. This is the differential joint here by the way that re-directs the torque from the drive shaft to the axles. At the end of each axle is a wheel and so there are two wheels being driven by the drive shaft. The wheel can be modeled as made up of three things, one being a thin layer of tread which we'll consider to be a hoop and it has own moment of inertia formula, and then there is the rest of the -- like the tire I suppose, and the side of the tire which is an annular ring with an outer and inner radius and then there is the wheel itself, the inner part of the wheel that everything is mounted on, the tire is mounted on I should say. That is going to be modeled as a disk with a radius equal to the inner radius of that annular ring. So, we're given the masses of all these things, the mass of the tread, the mass of the ring, and the mass of the wheel. So I have subscripts that I try to refer to those things, t for tread, r for ring, w for wheel, ds for drive shaft, and a for axle. We're given lots of data and so really this question is just a matter of being organized and keeping track of all the different things. So our moment of inertia in total of the entire drive train is going to be the sum of the moments of inertia of each component. So we have a drive shaft plus a moment of inertia of an axle and we have two tires, so that's why we have to multiply the moment of inertia of the tread by two. Then we multiply the moment of inertia of the ring by two and then the moment of inertia of the disk, the wheel, by two as well. Then for the drive shaft, a cylinder rotating about an axle down at center is the mass of the drive shaft multiplied by its radius squared divided by two, and it's the same formula for the axle. Then for the tread, hoop, has a formula of the mass of the hoop multiplied by its radius squared and it's not divided by two but it is multiplied by two because there are two treads, one for each wheel. Then we have the annular ring, and so we have the mass of the ring over two multiplied by its outer radius squared plus its inner radius squared, and we multiply that by two because there are two wheels. Then we have two times the moment of inertia of the wheel disk. So mass of the wheel times the radius of the wheel which is the inner radius of the annular ring, squared, divided by two. Then we plug in numbers. We took away all the divide by two's here because they cancel. So we have 30 kilograms drive shaft mass, multiplied by 3.2 centimeters converted into meters and square that, divide by two, plus 14 kilogram mass of the axle, multiplied by two centimeters converted into meters, squared, divided by two, plus two times the tread mass of ten kilograms times its radius of 0.33 meters, squared, and add to that two kilograms multiplied by the outer radius of the annular ring of 0.32 meters and square that, plus the inner radius of 0.18 meters and square that, plus the mass of the wheel, 15 kilograms times its radius of 0.18 meters squared. This gives us a moment of inertia of the whole drive train of 2.95176 kilogram meters squared. Then our job is to figure out what is the angular acceleration. So we know that the torque applied to the drive train equals its moment of inertia that we just found, multiplied by its angular acceleration and we're going to solve for alpha in a second. But first, let's substitute for the output torque because we're told that this drive train has a certain efficiency of 95 percent and we're told that the input torque is applied by the engine to the beginning of the drive shaft or drive train. So, the torque output is going to be equal to the torque input multiplied by its efficiency. So we'll substitute that in place of t naught and then we'll divide both sides by i to solve for alpha. So the angular acceleration will be the 200 Newton meters torque applied, multiplied by the 95 percent efficiency or 0.95 written as a decimal, divide by 2.95176 kilogram meter squared moment of inertia, giving us an angular acceleration of 64.4 radians per second squared.