Question
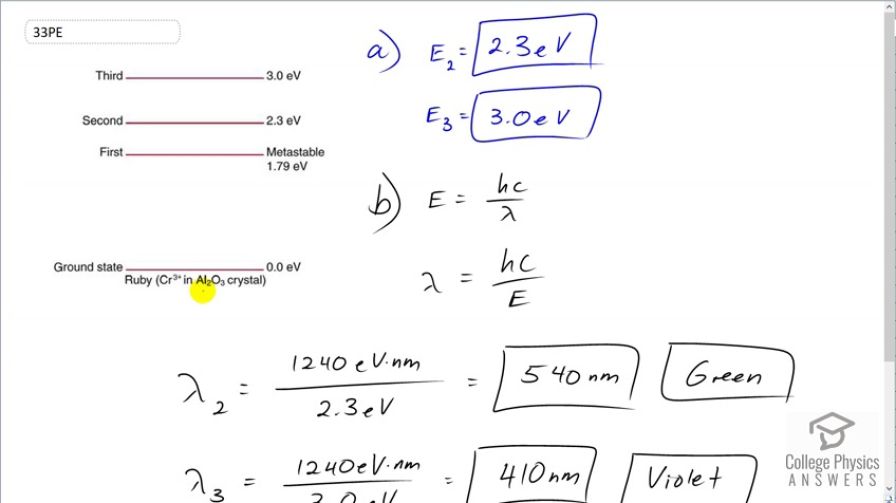
(a) What energy photons can pump chromium atoms in a ruby laser from the ground state to its second and third excited states? (b) What are the wavelengths of these photons? Verify that they are in the visible part of the spectrum.
Final Answer
-
- This is green.
. This is violet.
Solution video
OpenStax College Physics, Chapter 30, Problem 33 (Problems & Exercises)
vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. Here's a picture illustrating the energy levels of electrons in ruby in a ruby-chromium laser and we are told to say what is the energy of the second and third states beginning at ground state. So from ground state, it would take 2.3 electron volts to get to the second energy level whereas from the ground state, it would take 3.0 electron volts to get to the third energy level. And what wavelength photon would correspond to these energy differences. Well, energy of a photon is Planck's constant times speed of light divided by wavelength and so we can multiply both sides by λ over E to solve for λ. So the wavelength is hc over E. So the wavelength to get to the second energy level is gonna be 1240 electron volt nanometers; that's what the product hc is divided by 2.3 electron volts and these electron volts cancel leaving us with units of nanometers that's 540 nanometers; that's the color green. And to get to the third energy level, we expect an answer that is a shorter wavelength because shorter wavelengths have higher frequency and therefore higher energy since you could also express energy with the formula hf. And so getting a higher energy to the third energy level should require a shorter wavelength and sure enough, it's 410 nanometers which is the color violet.
