Question
Calculate the velocity of a star moving relative to the earth if you observe a wavelength of 91.0 nm for ionized hydrogen capturing an electron directly into the lowest orbital (that is, a to , or a Lyman series transition).
Final Answer
This is towards Earth.
Solution video
OpenStax College Physics, Chapter 30, Problem 55 (Problems & Exercises)
vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
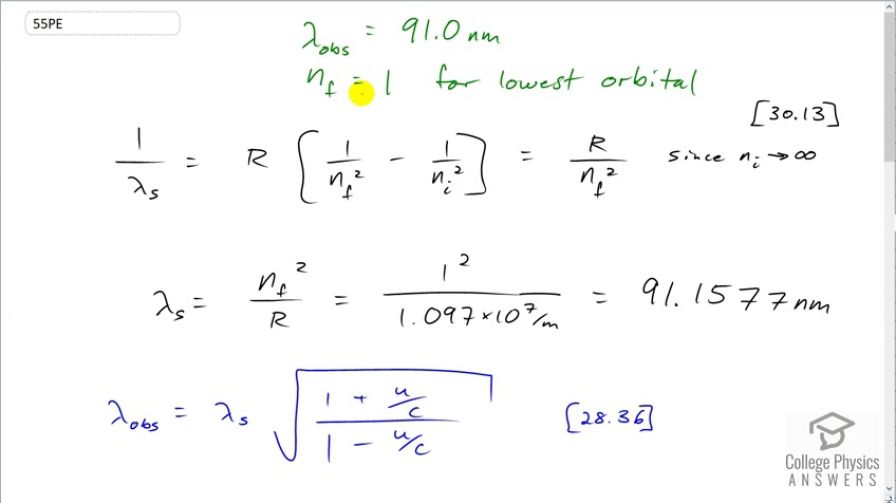
This is College Physics Answers with Shaun Dychko. Somehow we know that some light coming from a star was created by a hydrogen nucleus capturing a free electron which starts with an n i or an initial energy level of infinity; basically that's what happens when the electron is not attached to the nucleus at all. And it goes into the lowest orbital possible which is the minimum value for n f which is 1. So we can figure out what the wavelength should be based on this formula here and then compare that with what's observed and then use the relativistic Doppler effect formula which is from [28.36] and then solve for the velocity u to figure out how quickly the star is moving either towards or away from the Earth. Now we see that the wavelength that is emitted is 91.1577 nanometers; that's if you were at rest with respect to the capturing of the electron if you were at rest with respect to the hydrogen atom in other words, this is the wavelength that you would observe. And so the wavelength that's actually observed is 91 nanometers and is less than the source wavelength. And so this means that the object is or the star is coming towards us in order to have a blue shift of the wavelength; this is a blue shift because it's going to a smaller wavelength as a result of the velocity and well to figure this part out, we use this formula which is [30.13] and we know that the initial energy level is infinity and that makes this term become zero and so this reduces to r over n f squared and then when we take the reciprocal of both sides, we just flip both fractions and we get that the wavelength of the source then is n f squared over r. So that's 1 squared over Rydberg's constant which is 91.1577 nanometers. Then we use this relativistic Doppler effect formula and this is the observed wavelength—91.0— and this is wavelength of the source which is here and we have to solve this for u. So we'll divide both sides by λ s and then square both sides and switch the sides around, have the unknown on the left and you get this line here and then we multiply both sides by this denominator—1 minus u over c— and we end up with this line here. So we have 1 plus u over c; that's the numerator here equals the observed wavelength over the source wavelength squared times 1 and then minus that ratio times u over c. And then we bring this term to the left-hand side by adding it to both sides so that we are collecting the unknown factor, u, together on the left and then we also move the 1 to the right-hand side by subtracting it from both sides and then we factor out the u over c from this term and this term. And so that's u over c times 1 plus lambda observed over lambda source squared equals lambda observed or lambda source squared minus this 1. Then divide both sides by this binomial and multiply both sides by c and you end up with this. So the velocity then is the speed of light times lambda observed over lambda source squared minus 1 that's this whole thing and then that gets divided by this binomial here and now we plug in numbers to get our answer. So the velocity then is the speed of light times 91.0 nanometers observed divided by 91.1577 nanometers calculated wavelength of the source and we can leave this in units of nanometers because since they are both the same units, they will cancel anyway. And we square that ratio minus 1, take the same ratio squared plus 1 and then take the ratio of that and multiply it by the speed of light and you get negative 5.19 times 10 to the 5 meters per second. That is the velocity with which the star is moving towards the Earth; that's what the negative sign means and we expected that because a blue shift should mean the object is moving towards us.
