Question
Prove that the velocity of charged particles moving along a straight path through perpendicular electric and magnetic fields is . Thus crossed electric and magnetic fields can be used as a velocity selector independent of the charge and mass of the particle involved.
Final Answer
Please see the solution video.
Solution video
OpenStax College Physics, Chapter 30, Problem 67 (Problems & Exercises)
vote with a rating of
votes with an average rating of
.
Video Transcript
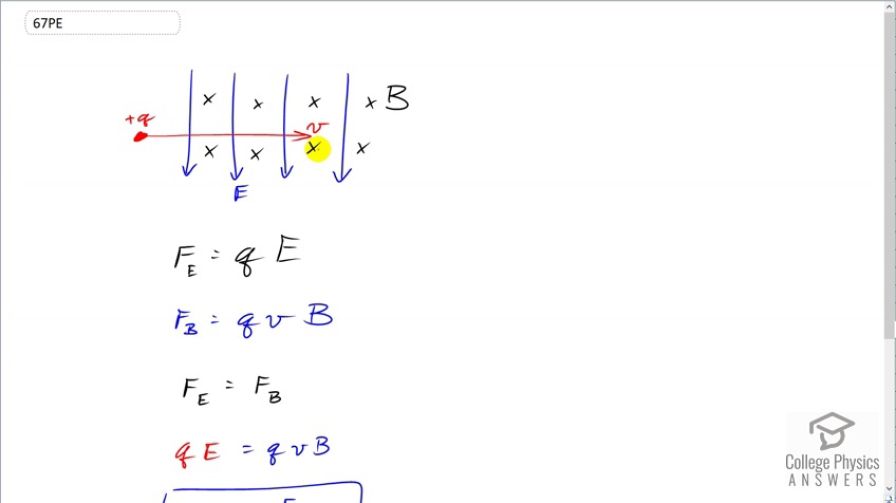
This is College Physics Answers with Shaun Dychko. A charged particle moving in the presence of a magnetic and electric field will— if these magnetic and electric fields are perpendicular to each other— there will be zero net force on this charged particle. And so the electric force in this picture will be directed downwards; the electric field direction points in the direction of force on a positive charge and the magnetic force is going to be upwards and we can figure that out using the right-hand rule by pointing our thumb in the direction of this velocity. and then our fingers are going to go into the page that's what this x's represent is magnetic field into the page and then our palm is directed upwards in the opposite direction to the electric field force downwards. OK. So the force due to the electric field is the charge times the field strength and the magnitude of the magnetic force is the charge times its velocity times the magnetic field strength. And then we can equate these two in order to have a velocity selector and then we can see that when we equate them and solve for v by dividing both sides by q B that the speed is gonna be the electric field strength divided by the magnetic field strength. And other speeds will have a different magnetic field strength force that will be different from the force applied by the electric field. The force applied by the electric field is the same for all velocities because it's not velocity-dependent; there's no factor v in this formula. But the magnitude of the force applied by the magnetic field is velocity-dependent and so it's only this particular velocity that will have a force equally up and down.