Question
Do the Balmer and Lyman series overlap? To answer this, calculate the shortest-wavelength Balmer line and the longest-wavelength Lyman line.
Final Answer
There is no overlap.
Solution video
OpenStax College Physics, Chapter 30, Problem 17 (Problems & Exercises)

vote with a rating of
votes with an average rating of
.
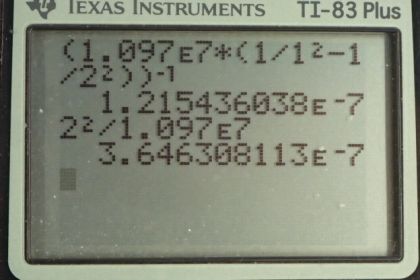
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. Equation [30.13] tells us the wavelength of the photons emitted during transitions of an electron between two states in the hydrogen atom. The Balmer series means that the final state will be 2 and for the Lyman series, the final state will be 1. So this is a lower ground state and so an electron going to a final state of 1 will experience a higher energy transition because it's arriving at a lower final state and therefore, a shorter wavelength. So the Lyman series has very short wavelength. The Balmer series, on the other hand, has a final energy level that is higher and so an electron going to this final state will have a longer wavelength and a smaller energy. When I'm making these comparisons, I'm assuming that the electron starts in some initial state, you know, 3 or more and if it goes from 3 to 2, that's a small energy transition or, in other words, long wavelength. whereas, from 3 to 1, is a high energy transition; in other words, a short wavelength. So to see if there's an overlap between these two series, what we need to do is find the shortest wavelength Balmer series emission that we can find and then compare that with the longest wavelength Lyman series wavelength. So to find the longest wavelength in the Lyman series, that means we wanna have the smallest energy transition and so the initial state we should take to be the smallest initial state that's possible which is 1 greater than the final state and the final state being 1 means that the initial state will have to be 2. And so let's figure out what the wavelength is when the initial state is 2 given a final state of 1 and this will tell us the maximum wavelength in the Lyman series or lowest energy emission. So I have solved this formula for lambda by taking both sides to the power negative 1 and I like to just leave this right-hand side as it is and wrap it in these brackets and put an exponent negative 1 there. And so the maximum wavelength of the Lyman series— subscript L means Lyman. So we have Rydberg's constant—1.097 times 10 to the 7 reciprocal meters— times 1 over the final energy level squared minus 1 over the initial energy level of 2 squared and then all that gets raised to the exponent negative 1 giving a maximum possible wavelength in the Lyman series of 121.5 nanometers. And then we'll find the shortest wavelength in the Balmer series and to do that, we want the largest energy transition possible. So the initial state, we'll take to be the largest that it can be which is infinity and the final state of course has to be 2; that's what you mean when you have a Balmer series; n f is 2. And so with n i being infinity, that means this term here will be zero because we are going 1 divided by a super big number and 1 divided by a number that's almost infinity is zero and so that's why the formula only has 1 term. and it's going to be well, maybe I can do an intermediate step there; we have 1 over λ equals R divided by n f squared when you get rid of this term here and make it zero and then you raise both sides to the negative 1 and you get this line here where you flip both sides. So we have λ minimum for the Balmer series is going to be the final energy level squared divided by Rydberg's constant. So that's 2 squared over 1.097 times 10 to the 7 reciprocal meters which is 364.6 nanometers. This means there is no overlap because this is the longest that the Lyman series can be and this is the shortest that the Balmer series can be. And so the Balmer series is gonna have this number or anything bigger and the Lyman series will have this number or anything smaller and so there will not be any overlap.