Question
(a) List all possible sets of quantum numbers for the shell, and determine the number of electrons that can be in the shell and each of its subshells.
(b) Show that the number of electrons in the shell equals and that the number in each subshell is .
Final Answer
Please see the solution video.
Solution video
OpenStax College Physics, Chapter 30, Problem 47 (Problems & Exercises)
vote with a rating of
votes with an average rating of
.
Video Transcript
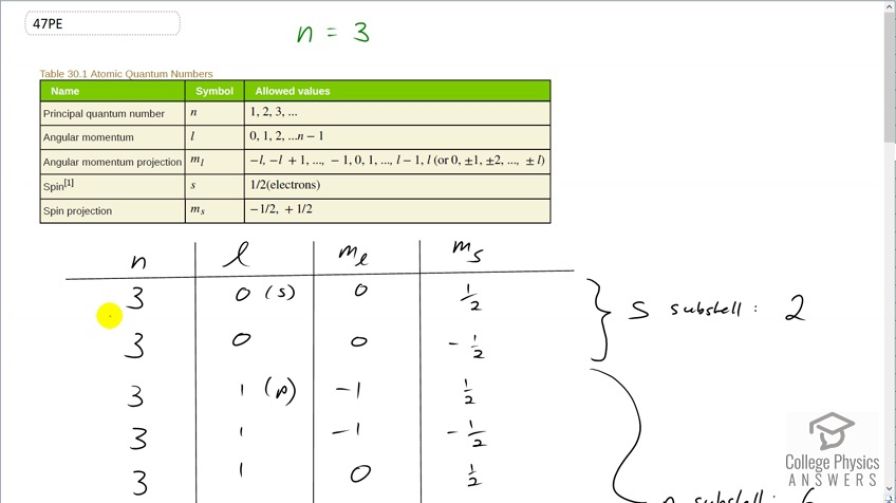
This is College Physics Answers with Shaun Dychko. We know that the principal quantum number is 3 and we are told to list all the possible quantum numbers for every electron in the n equals 3 state. So for the angular momentum quantum number, we know it can go from 0 up to n minus 1 so it can go 0, 1 or 2 and so in this column, you will see 0, 1 and 2 and I have put in brackets here the letter that corresponds to this angular momentum quantum number in spectroscopic notation. And this is the s-orbital and the p-orbital and then the d-orbital and then for each value of l, there are multiple values of the angular momentum projection quantum number and now when l is 0, m l has to be 0. And then for each value of n, l and m l, there are two possible values of the spin projection quantum number so positive a half and negative a half and it's always those two possibilities for m s. So with n equal to 3, l equal to 0 and m l equal to 0, we can have m s positive a half or we can have 3, 0, 0, negative a half and that's all you have in the s-subshell or l equals 0 subshell and so that corresponds to two electrons. Then in the p-orbital, we can have angular momentum projection quantum number of negative 1, 0 or 1 based on this constraint here which says that m l can be l which we are taking to be 1 right now so or negative l starting at and then increasing by 1's up until positive l so it can be negative 1, 0 or 1 for m l. And then for each of these three values, you can have positive a half or negative a half for the spin projection quantum number. And so we have 1, 2, 3, 4, 5, 6 possible electrons in this subshell, l equal to 1 or in other words, p-orbital. And then for the d-orbital when l equals to 2, m l can be negative 2, negative 1, 0, 1 or 2 and for each of those values of m l, you can have two values for the spin projection quantum number of a half or negative a half and this works out to 1, 2, 3, 4, 5, 6, 7, 8, 9, 10 possible electrons in the d-subshell. So this is 10 plus 6 plus 2 which is 18—total number of electrons— in the n equal to 3 state. And a formula for that is to say 2 times the principal quantum number squared and that will give the same answer, 18. In part (b), what's part (b) asking exactly? Oh yeah, show that this formula is true and so we have done that; we have already counted up the hard way that there are 18 electrons in the n equal to 3 state and indeed, this formula gives us that same correct answer. And then show that the number in each subshell is given by this formula. Alrighty. So we have counted up the number in each subshell by listing all the possible quantum number combinations. And so for the s-orbital, we have 2 times 2 times the angular momentum quantum number which is 0 plus 1 and this works out to 2. And for the p-orbital, we have 2 times 2 times l equal to 1 plus 1 and that equals 6 because 2 times 1 is 2 plus 1 is 3 times further 2 is 6. And then for the d-orbital, we have l equal to 2 and 2 times 2 is 4 plus 1 is 5 times 2 makes 10 and we have verified each of these based on listing out the hard way. There we go.