Question
Calculate the minimum amount of energy in joules needed to create a population inversion in a helium-neon laser containing of neon.
Final Answer
Solution video
OpenStax College Physics, Chapter 30, Problem 61 (Problems & Exercises)
vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
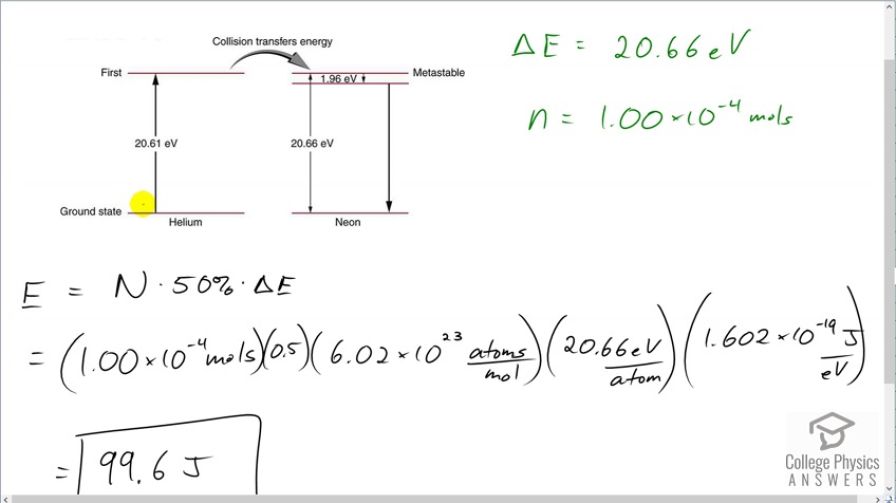
This is College Physics Answers with Shaun Dychko. A population inversion means that at least 50 percent of these helium atoms in this helium-neon laser are excited into their first energy state which is 20.61 electron volts above the ground state. And these excited helium atoms will then cause these neon atoms that they collide into to also become excited and then so on and then they will lose their energy with the emission of photons. So 20.66 electron volts of energy are needed to excite the neon and it's a little bit unclear how to answer this question because on the one hand, the pumping energy needs to only supply 20.61 electron volts whereas the neon needs 20.66 electron volts to get excited and that's a discrepancy of 0.05 electron volts and this discrepancy is usually supplied by thermal energy of the helium atoms and doesn't need to be supplied externally by whatever is priming this laser. But let's include this little bit of heat energy as well and so we'll say that the energy is 20.66 electron volts for each atom. And we have this many mol's of atoms which we convert into number of atoms by multiplying by Avogadro's number. And so the total amount of energy needed then is the number of helium atoms that need to be excited multiplied by 50 percent of them to create a population inversion and then times by the amount of energy per atom. So that's 1.00 times 10 to the negative 4 mols times 0.5 which is 50 percent, times 6.02 times 10 to the 23 atoms per mol times by 20.66 electron volts per atom and then convert this into joules by multiplying by 1.602 times 10 to the minus 19 joules per electron volt means we need 99.6 joules of energy.
