Question
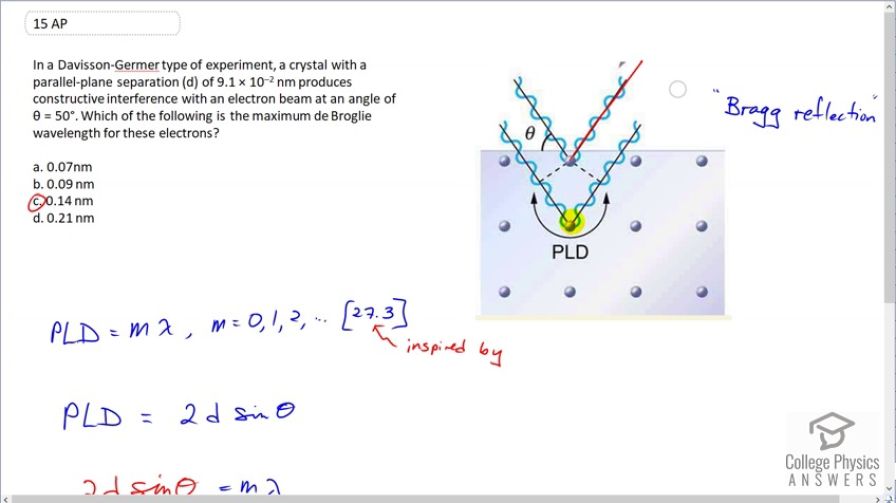
In a Davisson-Germer type of experiment, a crystal with a parallel-plane separation, , of produces constructive interference with an electron beam at an angle of . Which of the following is the maximum de Broglie wavelength for these electrons?
Final Answer
(c)
Solution video
OpenStax College Physics for AP® Courses, Chapter 29, Problem 15 (Test Prep for AP® Courses)
vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. An electron beam is incident on this crystal lattice and 1 electron gets reflected here and the next electron gets reflected from the plane below the initial plane. So here and we are told what the separation is between the two planes. And we want to know what is the path length difference between these two waves, so to speak; we are treating electron as waves here. And this is a right triangle and this angle here is Θ, the same as this incident angle, angle with respect to the plane and that makes this portion here of the triangle equal to this hypotenuse d times sin Θ. And now the total path length difference is going to be that plus itself again, on this other side, other side here. And so the total path length difference is going to be 2 times d times sin Θ, which is a little bit different than the formula [27.3] that we had before; before we were told that the path length difference between two beams going through two slits is d sin Θ, where d is the separation between slits. But that's no longer the path length difference in this case And so in this case the path length difference is 2 times the separation between these parallel planes and times sin Θ. So the path length difference is gonna be some integer multiplied by the wavelength to have constructive interference and we'll substitute 2d sin Θ in place of the path length difference and we solve for λ. So divide both sides by m and we get λ is 2d sin Θ over m. And once we are told that that we have this separation between the parallel planes so that's what d is and this construction interference at an angle of 50 degrees. And so we plug in and now we wanna know what the first constructive interference is and so that's why m is 1. And so we have 2 times 9.1 times 10 to the minus 2 nanometers times sin 50 over 1 which is 0.14 nanometers. And the reason we wanted a 1 for an m is we are looking for the maximum possible wavelength that works here. And so in order to maximum λ, we need to minimize this denominator and the minimum that it can be is 1. I mean, of course, you can do 0 but that's gonna make nonsense as this turns into undefined. So there we go; the answer is (c).
