Question
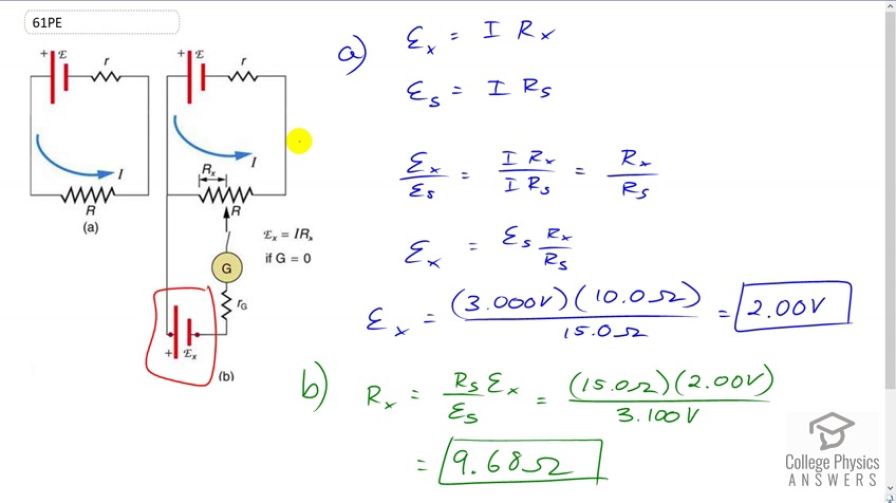
(a) What is the unknown in a potentiometer that balances when is , and balances when is for a standard 3.000-V emf? (b) The same is placed in the same potentiometer, which now balances when is for a standard emf of 3.100 V. At what resistance will the potentiometer balance?
Final Answer
Solution video
OpenStax College Physics, Chapter 21, Problem 61 (Problems & Exercises)
vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. This potentiometer is adjusted such that with an unknown EMF, Ex, we have a resistance Rx that we do know because we read off of our potentiometer here. And it’s multiplied by some current that we don’t know and don’t care about, because then we replace this unknown EMF with a standard EMF which we do know. And that’s going to equal the same current because we haven’t change this EMF up here. The same current multiplied by new resistance Rs which we get by adjusting this potentiometer. And we can divide these two on equations and get the unknown EMF divided by the standard EMF equals I times Rx over I times Rs. And the I is cancel and so this is the ratio of the resistances. And so we can multiply both sides by the Es, the standard EMF and we get the unknown EMF equals the standard EMF multiplied by the resistance when you have the unknown EMF divided by resistance with the standard EMF. And so this is three Volts times ten Ohms divided 15 Ohms. And this gives 2.00 Volts, must be the unknown EMF. Now, what if the standard EMF was instead 3.100 Volts, what would the resistance Rx be given a standard EMF of 3.1 Volts assuming that Rs bounces at the same resistance that I did before? And so we figured out what the Ex is the unknown EMF. Or at least it was unknown before. Now it’s two Volts, so we can substitute that in. We’re rearranging this formula here in blue and solving for Rx by multiplying both sides by Rs. So we multiply by Rs, multiply by Rs and we get Rx equals Rs times EMFx divided by EMF standard. So it’s 15 Ohms times two Volts divided by 3.1 Volts giving 9.68 Ohms.
