Question
Using the exact exponential treatment, find how much time is required to charge an initially uncharged 100-pF capacitor through a resistor to 90.0% of its final voltage.
Final Answer
Solution video
OpenStax College Physics, Chapter 21, Problem 73 (Problems & Exercises)
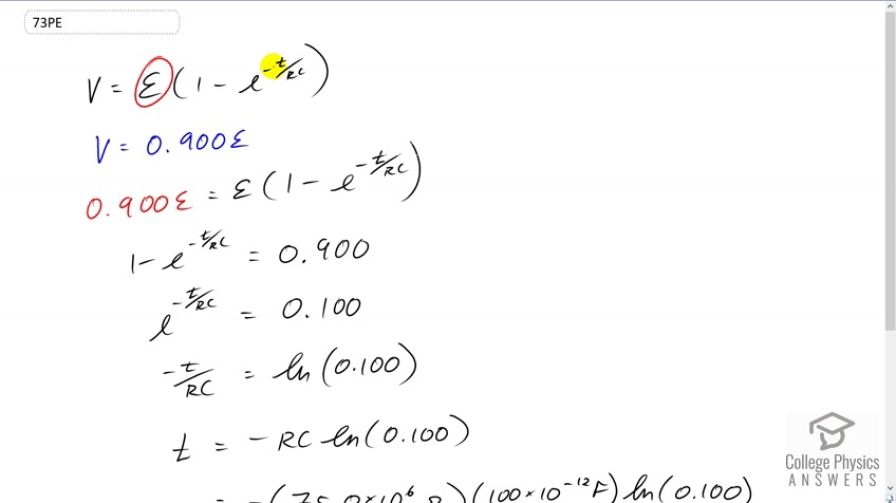
vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. The formula for the voltage of a discharging capacitor is the initial voltage multiplied by one minus e to the negative time over RC, resistance times capacitance. So we're told that the voltage is 90 percent of the initial voltage and so the question is how much time will that take to discharge the capacitor to 90 percent of what it started at. So we substitute 0.900 epsilon in place of V. And so the epsilon is cancel after we divide both sides by it. And we have one minus e to the negative t over RC equals 0.9. And we can take this term to the right side by adding it to both sides. And then we can subtract 0.9 from both sides. And we get e to the negative t over RC is 0.1. And then take the natural logarithm of both sides and you have negative t over RC on the left. And on the right, it's natural logarithm of 0.1. Then multiply both sides by negative RC. And then you have time is negative RC times natural log of 0.1. So that's negative 75 times ten to the six Ohms times 100 pico Farads and pico is the prefix meaning times ten to the minus 12. And then multiplied by natural logarithm of 0.1. And you 17.3 milliseconds.
