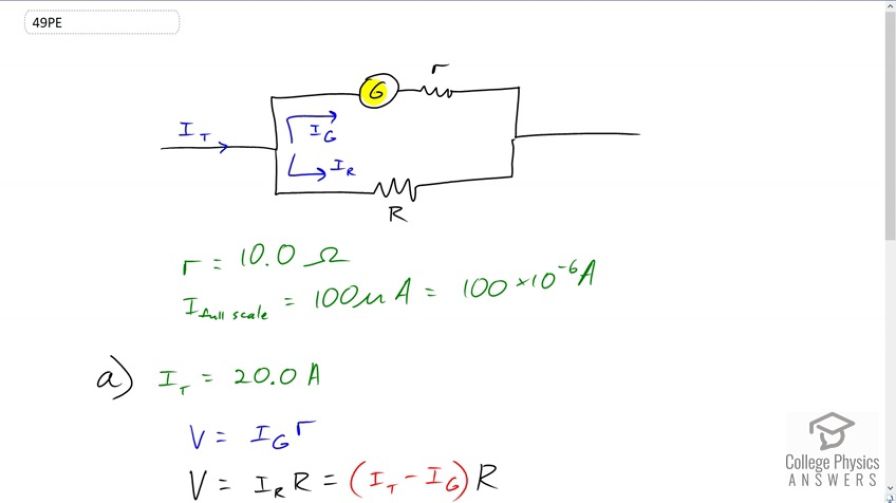
Question
Find the resistance that must be placed in parallel with a galvanometer having a sensitivity to allow it to be used as an ammeter with: (a) a 20.0-A full-scale reading, and (b) a 100-mA full-scale reading.
Final Answer
Solution video
OpenStax College Physics, Chapter 21, Problem 49 (Problems & Exercises)
vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. We have a galvanometer that has a sensitivity of 100 micoramps which means when there is full scale deflection of the needle in the galvanometer, there must be 100 microamps of current going through it. The internal resistance we're told is 10 ohms and our question is what should this shunt resistance be in order to have a full scale deflection when, A, we have a total current through the circuit of 20 amps or in B, when the total current in the circuit is 100 milliamps. Okay. So the voltage across the galvanometer is going to be the same as the voltage across the shunt resistance because they're connected in parallel and so this I subscript G is the current through the galvanometer multiplied by the internal resistance of the galvanometer is the voltage, and you could also say that the current across the shunt resistance multiplied by capital R is voltage across the shunt resistor. This I subscript capital R is going to be the total current going into this junction minus whatever is taken up through the galvanometer. So I've replaced it with that. That's using the junction rule. So I t for total has to equal current to the galvanometer plus the current through the shunt resistance. We can solve for the shunt resistance by subtracting I G from both sides and then switching the sides around. You get I t minus I G, okay? That's multiplied by capital R and so since these are connected in parallel, these have the same voltage across them and so we can equate them which we do here. We'll solve for capital R by dividing both sides by I t minus I G. So the shunt resistance is 100 microamps times 10 ohms, that's the sensitivity of the galvanometer multiplied by its internal resistance divided by the current total at which full scale deflection is meant to occur which is 20 amps in part A, minus 100 times ten to the minus six amps. That gives 5.00 times ten to the minus five ohms. Now in part B, It's exactly the same idea but now there's just a different value for the total current at which full scale deflection of the galvanometer should occur. So we use the same formula but substitute in 100 milliamps which is 100 times ten to the minus three amps instead of 20 amps like before. In this case we get 10.0 milliohms.
Comments
its tough to follow your convoluted algebra. I get that you are trying to solve it entirely then add numbers, but took me several minutes to figure out that you could also just solve for R using the voltage that we could also very easily find... so instead of setting them equal to each other find the voltage, then solve for the knowing V, It, and Ig makes it easier to follow.


