Question
Suppose you measure the terminal voltage of a 3.200-V lithium cell having an internal resistance of by placing a voltmeter across its terminals. (a) What current flows? (b) Find the terminal voltage. (c) To see how close the measured terminal voltage is to the emf, calculate their ratio.
Final Answer
Solution video
OpenStax College Physics, Chapter 21, Problem 51 (Problems & Exercises)
vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
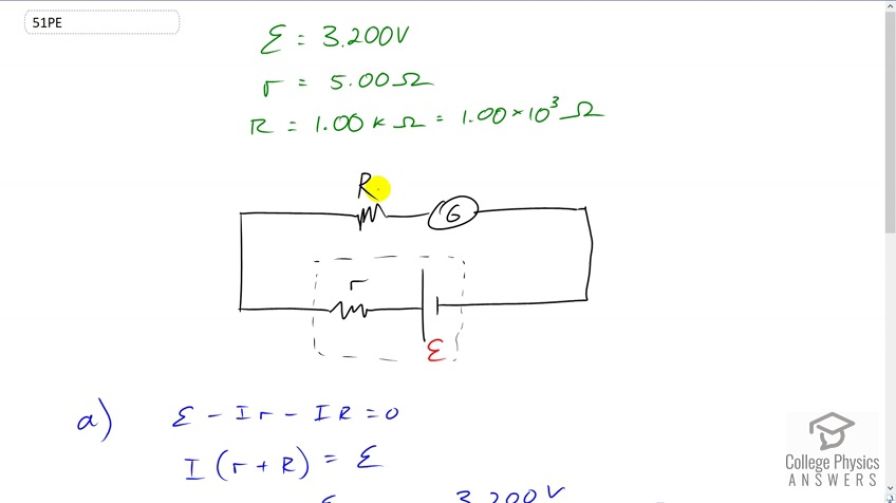
This is College Physics Answers with Shaun Dychko. We have a lithium battery with an EMF of 3.200 volts and an internal resistance of five ohms and we use a voltmeter to measure its voltage. The voltmeter has an internal resistance of one kilo-ohm which is one times ten to the three ohms. So the first question is what current is flowing through the voltmeter while it's doing its measurement? We can use the loop rule and start from here, say, and we have this -- we can traverse in this direction and have the current going this direction as well, clockwise. We'll have an increase in potential and we'll call that scripted E and then minus the current multiplied by the internal resistance of the battery, little r, and then minus the current multiplied by the resistance of the voltmeter, and all that equals zero. So we can solve for I by adding I r to both sides and then adding I capital R to both sides as well, then factoring out this common factor capital I. So we have I times little r plus bigR equals E and then divide both sides by this total resistance. So the current is going to be the EMF divided by the total resistance, so that's 3.2 volts divided by five ohms plus one times ten to the three ohms which gives 3.18 milliamps. Now when that current is flowing, the terminal voltage measured by the voltmeter is going to be the EMF minus the potential drop across the internal resistance of the battery. So that's 3.2 volts minus 3.1841 times ten to the minus three amps which is this current we found before, multiplied by the internal resistance of five ohms, giving 3.18 volts. So we can see that the act of measuring the voltage of the battery changes the terminal voltage of the battery. Ideally we would measure 3.2 volts but because the voltmeter needs to draw some current, there's going to be a drop across the internal resistance of the battery causing it to have a terminal voltage of only 3.18. Comparing that to the EMF we can divide the two and we get 0.995. So it's pretty much the same, it's 99.5% of the EMF.
