Question
A heart defibrillator being used on a patient has an time constant of 10.0 ms due to the resistance of the patient and the capacitance of the defibrillator. (a) If the defibrillator has an capacitance, what is the resistance of the path through the patient? (You may neglect the capacitance of the patient and the resistance of the defibrillator.) (b) If the initial voltage is 12.0 kV, how long does it take to decline to ?
Final Answer
Solution video
OpenStax College Physics, Chapter 21, Problem 69 (Problems & Exercises)

vote with a rating of
votes with an average rating of
.
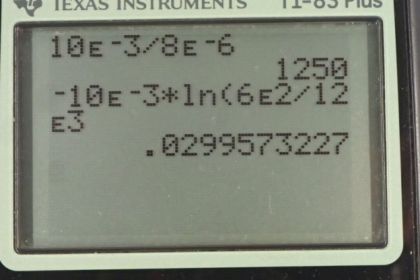
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. The time constant for this heart defibrillator is ten milliseconds, that’s ten times ten to the minus three seconds. And it has a capacitance of eight micro Farads. Now the final resistance of the RC Circuit in this defibrillator will be the time constant equals resistance multiplied by the capacitance and we’ll divide both sides by C to solve for R. So R is tau over C. So that’s ten times ten to the minus three seconds divided by six times ten to the minus six Farads giving us 1.25 kilo Ohms. Part b says given some initial voltage of 12 kilo Volts, how long will it take to reach the voltage of six times ten to the two Volts? So, this is the formula for the discharging capacitor. And we’ll divide both sides by V naught, the starting voltage. And so e to the power negative time over time constant equals the final voltage divided by the initial voltage. And then take the natural logarithm of both sides and in which case the left side becomes negative t over tau. On the right side is natural logarithm of V over V naught. And then multiplied both sides by negative tau and you get the time. So it’s the negative of the time constant, ten times ten to the minus three seconds times the natural logarithm of times six times ten to the two Volts divided by 12 times ten to the three Volts, giving us 30.0 milliseconds.