OpenStax College Physics, Chapter 21, Problem 25 (Problems & Exercises)

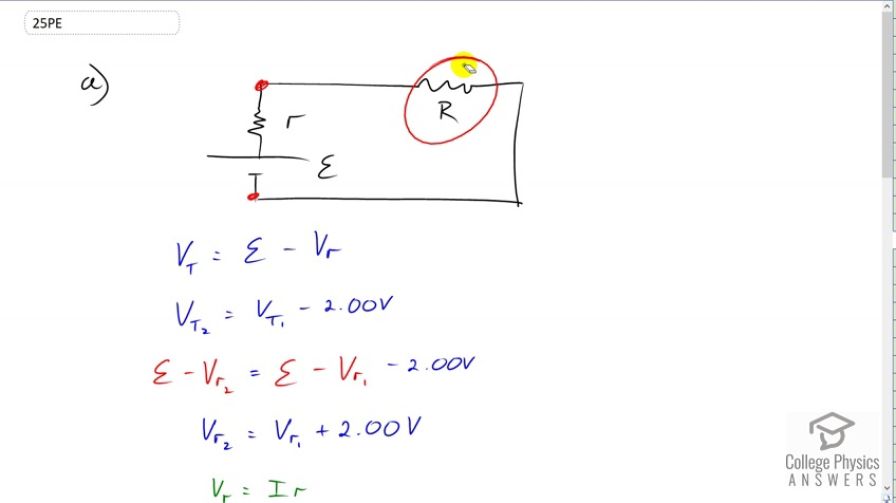
This is College Physics Answers with Shaun Dychko. We have a circuit here with an EMF and internal resistance. There must be some external resistance as well although we don't know much about it and it doesn't really matter. Now what we are told is that the terminal voltage across this battery reduces by two volts when the current increases by 5 amps. So we're going to use that information to figure out what this internal resistance must be. We know that terminal voltage is EMF minus the voltage across the internal resistance. So that's why I wrote V subscript little r to represent the voltage across the little internal resistance. The voltage in the terminal in the second case equals the terminal voltage in the first case minus two. This is an algebraic way of saying the terminal voltage reduces by two volts in the second case compared to the terminal voltage in the first case. We'll substitute from here in place of V t two and V t one. We'll write EMF minus voltage across the internal resistance in the second case equals the same EMF minus voltage across the internal resistance in the first case. The EMFs make zero when you subtract them from both sides and then we multiply both sides by negative one just to get rid of all these minus signs. We get V R two equals V R one plus two. So when the terminal voltage reduces in the second case it's because the voltage across the internal resistance has increased by two volts. Then we -- so now we have an equation involving the internal resistor which is good but we want this little r to appear in our equation because that is what we're trying to solve for. So we can do that by replacing this V subscript r with current multiplied by internal resistance. So in the second case we have I two multiplied by internal resistance equals the first case which is going to be substituted with I one times internal resistance and plus two copied there. Then get the little r's on the same side by subtracting I one little r from both sides. So we have I two r minus I one r equals two and then factor out the r and you get this line here. Divide both sides by I two minus I one, and you have two volts divided by I two minus I one. Now we don't know what I two nor I one are but we do know that their difference is five amps because we're told that I two is five amps more than I one. So that means I two minus I one has to be five. So two over five is 0.400 ohms and that is the internal resistance. Now in part B we're asked if we can determine EMF and we cannot because the best we ca do is write down these four equations. The terminal voltage in case one is EMF minus the current in case one times internal resistance. The terminal voltage in case two equals the same EMF minus the current in case two multiplied by internal resistance. The terminal voltage in case two is two volts less than the terminal voltage in case one. The current in case two is five amps more than the current in scenario one. That's four equations but there are five unknowns. There is one, two, three, four, and then five things that we don't know. So for five unknowns you need to have five equations. You need to have as many equations as you have unknowns in order to solve a system of equations. There are only four equations with five unknowns so we cannot solve it completely.