Question
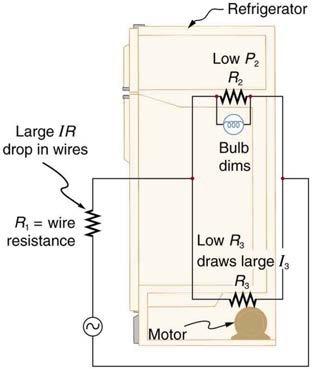
Refer to Figure 21.7 and the discussion of lights dimming when a heavy appliance comes on. (a) Given the voltage source is 120 V, the wire resistance is , and the bulb is nominally 75.0 W, what power will the bulb dissipate if a total of 15.0 A passes through the wires when the motor comes on? Assume negligible change in bulb resistance. (b) What power is consumed by the motor?
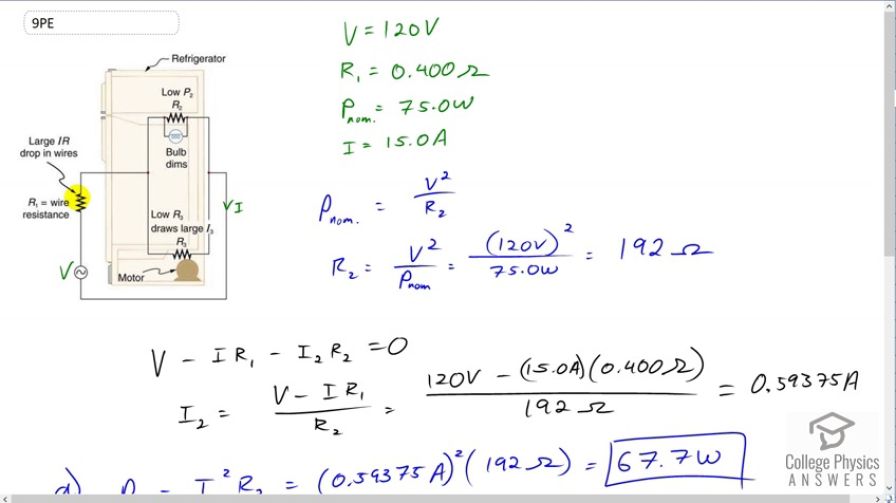
Final Answer
Solution video
OpenStax College Physics, Chapter 21, Problem 9 (Problems & Exercises)
vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. In this circuit for a refrigerator we have the power source which is the plug in the wall, and then a resistor here representing the resistance of the wires of 0.4 ohms. Then there is a parallel circuit of the bulb and the motor of the refrigerator. This bulb is drawn a bit funny. It would appear that there are two things in parallel, a resistor and then the bulb, but that's not the case. This is one thing and it's just an unusual way of drawing it where they're the same. This is the bulb and we're going to represent it by a resistor. So this is one resistance. Okay. So our job is to figure out what is the current through the bulb when the motor is turned on. We're told that there are 15 amps of current going through the wires in total when the motor is on. So the current out here is called I, it's 15 amps. We're told the voltage is 120 volts and we're told the nominal power of this bulb is 75 watts. What the word nominal means is that if you had just the power source and the bulb, this is R two, then in this case the power would be 75 watts. So this is the -- when they stamp the number 75 on the bulb and sell it in the store in a box that says this bulb is 75 watts, this is the test that they did to measure that wattage. They have the power source and the bulb isolated in one circuit. So what that means is we can figure out its resistance by saying the nominal power is the 120 volts that would have been used to create this measurement of 75 watts and divided by the resistance after you square the voltage, of course. So we can solve this for R two by multiplying both sides by R two over nominal power. We have R two is voltage squared over nominal power. So that's 120 volts squared, divided by 75 watts, which is 192 ohms. Then we can use that information in our Loop Rule and so we're going to have a loop that begins at this power source, stays at this side and then goes this direction. That's going to be a gain in voltage, and then we're traversing this resistance in the direction of the current and so that's a drop in potential. So that's the current multiplied by R one, and then we'll go through the bulb and then that's going to be another drop in potential. The current through the bulb I two multiplied by the bulb's resistance R two, then all of that is going to equal zero because that's what the loop rule says, conservation of energy. Then we solve this for I two by adding I two R two to both sides and then dividing both sides by R two and we solve for I two. So I two is V minus I R one over R two. 120 volts minus 15 amps times 0.4 ohms divided by 192 ohms that we calculated up here. This gives 0.59375 amps. Now the reason that's useful is because we can take that current and square it and multiply by the resistance to get the power. So we take that current square it, multiply it by 192 ohms and this gives 67.7 watts. So we expected a number here that was less than the nominal power of the bulb because the voltage across it is going to be less than 120 because with so much current going through the wires here, there's going to be a potential drop across this resistance and so that leaves well, the voltage that's going to go across this bulb will be 120 minus whatever the potential drop across the wire resistances. So we expected some number less than 75. So that's just a good reality check that you should do with your answers if you can. Then power three, the power consumed by the motor, there's two ways to answer that. One is we could figure out what is the voltage across the motor, and that's going to be 102 volts minus 15 times 0.4 and that's 120 minus potential drop across this resistance. Then figure out what the current is to the motor using the same method we used for finding the current across the bulb and then figure out the -- from that, figure out the resistance of the motor and then you can go I squared R for the motor and figure out its power. That would be one method. But since I've already done that kind of method already, showing a different method for part B. So this different method is to say that there's this total power dissipated or consumed from the power source which is the current provided times the voltage of the power source. From that, we'll take the total of the power consumed in the wires plus the power consumed in the bulb and what's left over must be the power consumed by the motor because that's the only thing left in the circuit to account for this total power consumption. So we have 15 amps times 120 volts minus 15 amps squared times 0.4 ohms, that's the power consumed by the wires, plus 67.6875 watts which is the answer for part A, power consumed by the bulb, and then this leaves us with 1.64 kilowatts must be the power consumed by the motor.

