Question
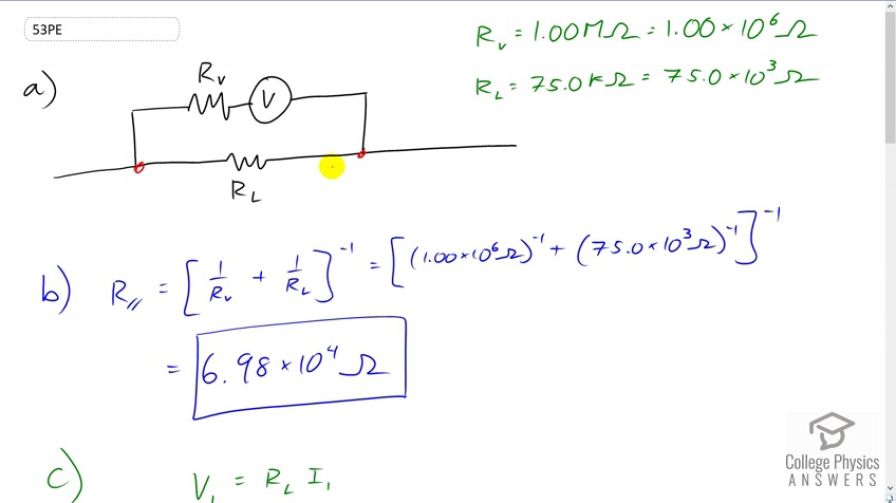
A voltmeter is placed in parallel with a resistor in a circuit. (a) Draw a circuit diagram of the connection. (b) What is the resistance of the combination? (c) If the voltage across the combination is kept the same as it was across the resistor alone, what is the percent increase in current? (d) If the current through the combination is kept the same as it was through the resistor alone, what is the percentage decrease in voltage? (e) Are the changes found in parts (c) and (d) significant? Discuss.
Final Answer
- See solution video for the circuit schematic
Solution video
OpenStax College Physics, Chapter 21, Problem 53 (Problems & Exercises)
vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. We have a voltmeter put in parallel with some load resistance and here's the circuit diagram describing that. This voltmeter has some resistance R subscript V for voltmeter and it is one times ten to the six ohms and the load has a resistance of 75 kilo-ohms which is 75 times ten to the three ohms. So the first question is what is the total resistance of this circuit from here to here? The answer is that we add them as parallel resistors and so we have the reciprocal of the sum of the reciprocals of each resistance. So reciprocal means exponent negative one, so we can write this one over R V as one times ten to the six ohms to the power negative one. We add to that 75 times ten to the three ohms to the negative one, take that total and then raise that total to the exponent negative one. This gives 6.98 times ten to the four ohms. Then in part C, we're told assume that the voltage across this load resistance is the same before and after you add the voltmeter. Now, the voltmeter is going to draw some current and reduce the total resistance from here to here, thereby would reduce the current across this load resistance. But we're told that there's going to be a compensating increase in the current such that the voltage across the load stays the same. So by what factor is that current increase in order to make that happen, to make these voltages the same? So in the first case with no voltmeter, the voltage across it, across the load, will be the resistance of the load multiplied by the initial current. In the second case with the voltmeter added to the circuit, we're going to have this total parallel resistance multiplied by some different current I two. We're told that voltage one and voltage two are meant to be the same and so that means we can equate these two. So we have R l I one equals R total parallel I two. Then take this ratio I two over I one by multiplying both sides by -- we have to divide by I one and then divide by R parallel as well. So we're multiplying by one over that. Then R parallel cancels here and we're left with I two over I one and then on the left hand side the I ones cancel leaving us with R l over R parallel. So I two over I one is R load over R total in parallel. So that's 75 times ten to the three ohms divided by 6.9767 times ten to the seven ohms, giving us 1.075. So I two is one plus 0.075 times I one. We're just having a long-winded way of saying increase by seven and a half percent. So this works out to I one plus 0.075 times I one. So this is the increase in I one and as a percentage the factor 0.075 is 7.50 percent. So the current has to increase by seven and a half percent when you add the voltmeter in order to keep the voltage across the load the same as before. In part D, we're told keep the current the same and by what factor will the voltage have to change such that that's true? So the current through the combination is the same as it was before the voltmeter was added and so what percentage decrease in voltage occurs? So, these are the same as the way we started part C but now we cannot say V one equals V two. Instead we say the I one equals I two and let's just give it a letter with no subscript because it doesn't need it since one and the two subscripts are the same. We'll just call it I and so I replaced I one and I two with just the letter I. Then we can divide these voltages V two over V one and we have I R parallel divided by I R load and the I's cancel. Then we have the total resistance when the voltmeter is added, so that's 6.9767 times ten to the four ohms divided by the resistance of the load, 75 times ten to the three ohms which is 0.930227. So V two is decreased from V one by this difference which is 0.06977 which as a percentage is 6.98 percent. So voltage after the voltmeter is added is going to decrease by 6.98 percent compared to when there is no voltmeter.

