Question
What are the largest and smallest resistances you can obtain by connecting a , a , and a resistor together?
Final Answer
Solution video
OpenStax College Physics, Chapter 21, Problem 3 (Problems & Exercises)

vote with a rating of
votes with an average rating of
.
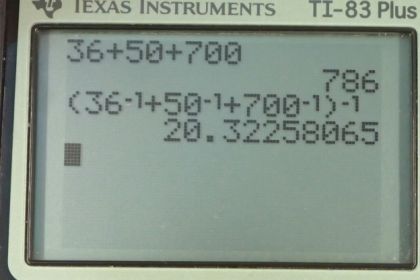
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. To get the largest resistance with a collection of resistors you have to connect them in series. The total series resistance will be the sum of each resistance added together directly. So we have 36 ohms plus 50 ohms plus 700 ohms, making 786 ohms in total. The minimum resistance you get by connecting them in parallel. The total parallel resistance will be the reciprocal, and that's what the power of negative one means there, take the reciprocal of the sum of the reciprocals of each resistance. So we have 36 to the power of one, negative one I should say, plus 50 ohms to the power of negative one, plus 700 ohms to the power of negative one. Add all that together, take the reciprocal of that sum and you end up with 20.3 ohms. That's the minimum total resistance possible.