Question
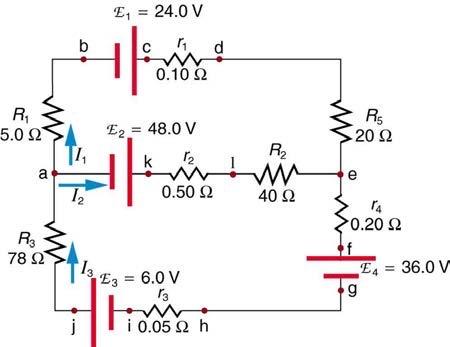
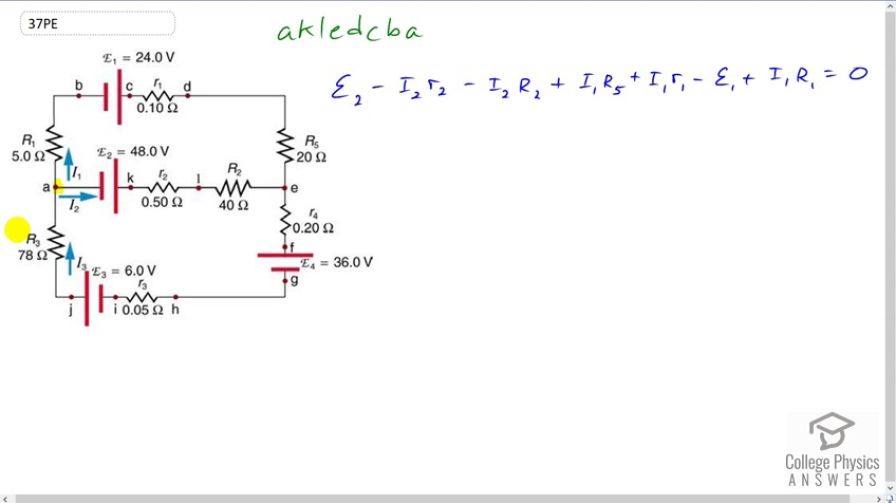
Apply the loop rule to loop akledcba in Figure 21.52.
Final Answer
see solution video for the Kirchoff's Law loop rule equation.
Solution video
OpenStax College Physics, Chapter 21, Problem 37 (Problems & Exercises)
vote with a rating of
votes with an average rating of
.
Video Transcript
This is College Physics Answers with Shaun Dychko. This question asks us to apply the Loop Rule to a loop in this circuit starting at point a and going to point k and then l, e and then up to d and c and b and then back to a. So we’re traversing the loop in this direction here. And this is going to be our equation. And let me explain where I get each of the terms. So we start at point a and we end at point k, first of all. And so we are traversing the loop from the negative to the positive terminal of an EMF. This is a positive change of potential. So we have positive EMF two here and then we’re traversing the loop in the same direction as the current I2 through this resistor little r2. And so it’s a reduction of potential in that case. And so it’s minus I2 times little r2. And then likewise for this resistor going across the resistor in the direction of the current. And so it’s a minus I2 times capital R2. And then through this resistor, our traversal direction is opposite to the direction of the current because I1 is going to the right here. It’s going up to the left we’re told. It goes to the right on the top. It goes down on the right side. And so, when you traverse a loop in the opposite direction to the current across a resistor, this is a gain in potential. And so we have a positive I1 multiplied by capital R5. And then likewise across the little r1, we’re traversing in the opposite direction to the current across this resistor and so that’s a positive I1 times little r1. Going from the positive to the negative terminal of an EMF is a drop in potential. So that’s negative EMF one. And then traversing capital R1, this is a positive I1 times capital R1 ‘coz we’re traversing in the opposite direction to the current through capital R1, as well. And all of this equals zero because we reached our starting point.