Question
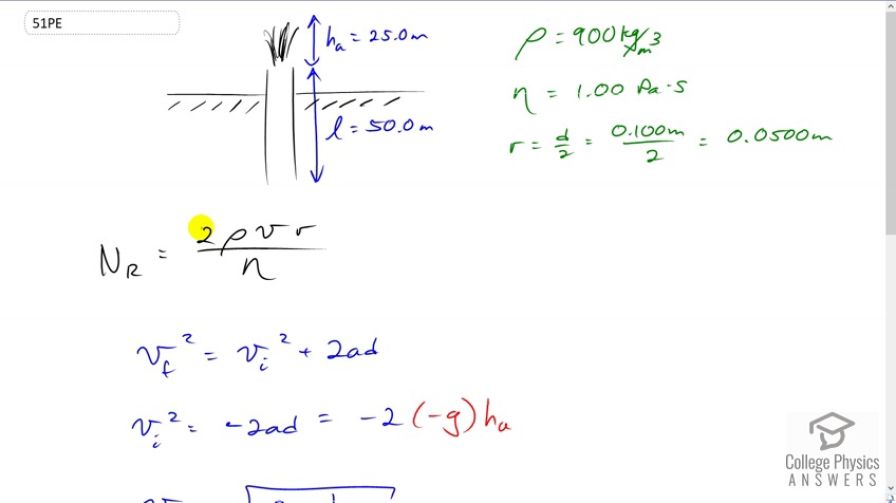
Verify that the flow of oil is laminar (barely) for an oil gusher that shoots crude oil 25.0 m into the air through a pipe with a 0.100-m diameter. The vertical pipe is 50 m long. Take the density of the oil to be and its viscosity to be (or ).
Final Answer
Since the Reynold's number is less than 2000, this flow is laminar.
Solution video
OpenStax College Physics, Chapter 12, Problem 51 (Problems & Exercises)
vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. To figure out if the flow of oil through this pipe is laminar, we need to calculate the Reynolds number. The Reynolds number is two times the density of the oil times its speed through the pipe times the radius of the pipe divided by the viscosity of the oil. So we’re given some information here, density, Reynolds number and the radius which is diameter divided by two. The only thing that’s gonna be complicated to calculate is the speed of the oil through the pipe, v. Well we’re gonna use the fact that the oil goes from the mouth of the pipe, 25 meters in the air, in order to calculate what the speed must be. So using this kinematic formula that the final speed squared equals initial speed squared plus 2ad, we know that the final velocity at the very top is zero. And in that case this term is zero, and we can subtract 2ad from both sides, and then switch the sides around, we get the initial speed squared which is the speed here at the mouth, which is just the v with no subscript in this Reynolds number formula. That squared is negative two times acceleration times displacement. So the acceleration is negative g, and the displacement is this height above the mouth that it sprays in the air, h subscript a for air, 25 meters. So we’ll take the square root of both sides and then we get v is square root 2g ha, so we substitute that in for v in our Reynolds number formula and we do that here, and then we plug in numbers. So we have two times 900 kilograms per cubic meter times square root of two times 9.81 meters per second squared times 25 meters times 0.05 meters, radius of the pipe, divided by one Pascal second, viscosity of the oil, which is 1993. So this is less than 2000, so it’s barely laminar.
