Question
A small artery has a length of and a radius
of . If the pressure drop across the artery is
1.3 kPa, what is the flow rate through the artery? (Assume that the temperature is .)
Final Answer
Solution video
OpenStax College Physics, Chapter 12, Problem 33 (Problems & Exercises)
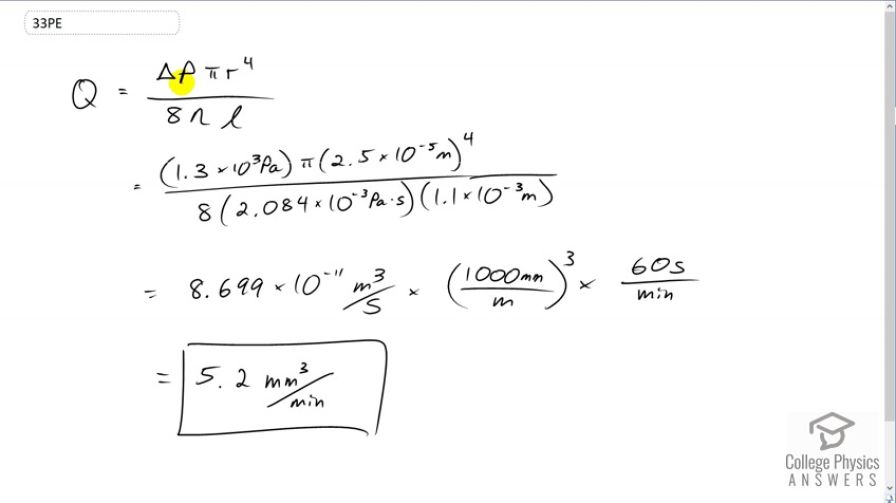
vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. The flow rate along a tube is given by Poiseuille's Law which is that the flow rate will be the difference in pressure at the two ends of the tube times pi, times the tube's radius to the power of four divided by eight, times the viscosity of fluid flowing, times the length of the tube. So that's 1.3 times ten to the three pascals times pi, times two and a half times ten to the minus five meters radius to the power of four, divided by eight, times 2.084 times ten to the minus three pascal seconds which is the viscosity of blood at 37 degrees Celsius, and then times 1.1 times ten to the minus three meters length of the tube. So, this works out to this number which we convert into something that is more meaningful by converting the cubic meters into cubic millimeters, and then convert the seconds into minutes. This works out to 5.2 cubic millimeters per minute.
