Question
Calculate the Reynolds numbers for the flow of water through (a) a nozzle with a radius of 0.250 cm and (b) a garden hose with a radius of 0.900 cm, when the nozzle is attached to the hose. The flow rate through hose and nozzle is 0.500 L/s. Can the flow in either possibly be laminar?
Final Answer
- . This flow is turbulent.
- . This flow is turbulent.
If the flow rate was a bit less than , then , in which case the flow would be laminar in the hose. The nozzle would require a significantly lesser flow rate.
Solution video
OpenStax College Physics, Chapter 12, Problem 53 (Problems & Exercises)
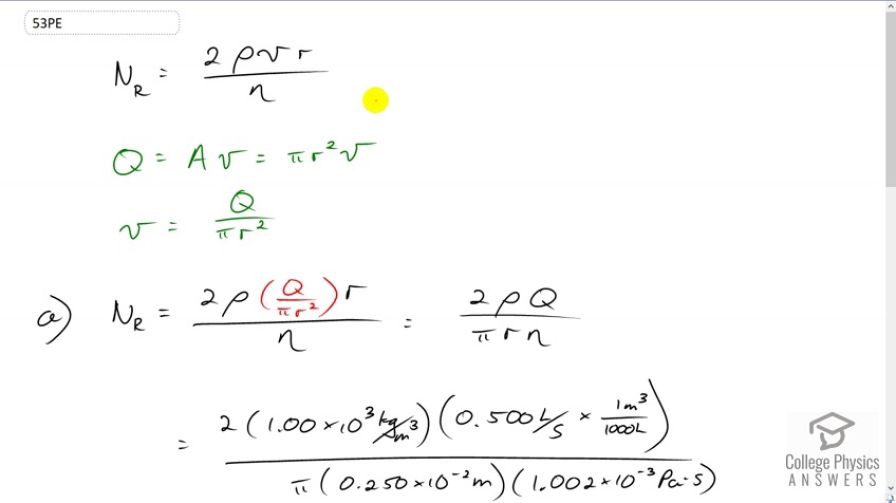
vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. We’ll need to calculate the Reynolds number for the water through the hose and through the nozzle, and if it’s greater than 3000, then we’ll say that the flow must be turbulent. So we have two times the density of the water times its speed through the hose or the nozzle, times the radius divided by the viscosity of water. Now we need to calculate the speed of the water by using this volume flow rate that we’re given, 50 or 0.5 liters per second, and that’s going to equal the cross sectional area of the pipe times the speed. So we can divide both sides by the area which is pi times radius squared in order to figure out v. So v is the volume flow rate divided by pi r squared, so we substitute that in for v in the Reynolds number formula. So considering the nozzle first, the Reynolds number in the nozzle is two times density times Q over pi r squared times r over nu, and the r squared here multiplied by this r, that’s going to work out to r to the power of one in the denominator. So Reynolds number is 2 rho Q over pi r nu. So we have two times the density of water, 1000 kilograms per cubic meter, times 0.5 liters per second converted into cubic meters per second by multiplying by one cubic meter for every 1000 liters, then we divide by pi times 0.25 times ten to the minus two meters, which is the radius of the nozzle, times 1.002 times ten to the minus three Pascal second, viscosity of water at about 20 degrees Celsius, and this works out to this huge number, 1.27 times ten to the five, which is much much greater than 3000 so this flow will definitely be turbulent. Now in the garden hose portion, the speed of the water will be smaller and we have this same formula that applies. And so we substitute new numbers in there, the only thing being different is this radius of the hose is 0.9 times ten to the minus two meters, and this makes a Reynolds number of 35300 which is a lot less than we have before of the nozzle, but nevertheless still much more than 3000 and so the flow is still turbulent. Now if the flow rate was a bit less than one seventeenth of what it is, now I get that one over 17 because this number is about 17 times 2000, and 2000 is the upper limit Reynolds number to have laminar flow. So if its flow rate was reduced to one seventeenth of what it was, then in that case the Reynolds number will be a bit less than 2000 in the garden hose in which case the flow will be laminar. In the nozzle, the volume flow rate would have to be reduced by significantly even more to get a laminar flow.
