(a) Estimate the time it would take to fill a private swimming pool with a capacity of 80,000 L using a garden hose delivering 60 L/min. (b) How long would it take to fill if you could divert a moderate size river, flowing at $5000{\text{ m}}^3\text{/s}$, into it?

Video Transcript

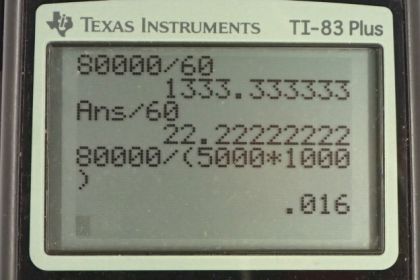
This is College Physics Answers with Shaun Dychko. We’re going to calculate the amount of time to fill a swimming pool with a garden hose. Now the volume flow rate through the garden hose is the volume that comes out of it divided by the time it takes, and we can solve for t by multiplying both sides by t over Q. And we have time is the total volume divided by Q. So the total volume is going to be that of the swimming pool, 80000 liters. And we’ll divide that by the flow rate of 60 liters per minute and this gives 1333.3 minutes but we’ll convert that into hours by multiplying by one hour for every 60 minutes, and this gives 22 hours. Now if there was instead a river flowing with a volume rate of 5000 cubic meters per second, we have 80000 liters divided by 5000 cubic meters per second, which we then have to convert into liters per second by multiplying by 1000 liters for every cubic meter, and this works out to 0.016 seconds, so it’ll be almost immediately filled.