Question
(a) Find the average time required for an oxygen molecule to diffuse through a 0.200-mm-thick tear layer on the cornea. (b) How much time is required to diffuse of oxygen to the cornea if its surface area is ?
Final Answer
Solution video
OpenStax College Physics, Chapter 12, Problem 65 (Problems & Exercises)
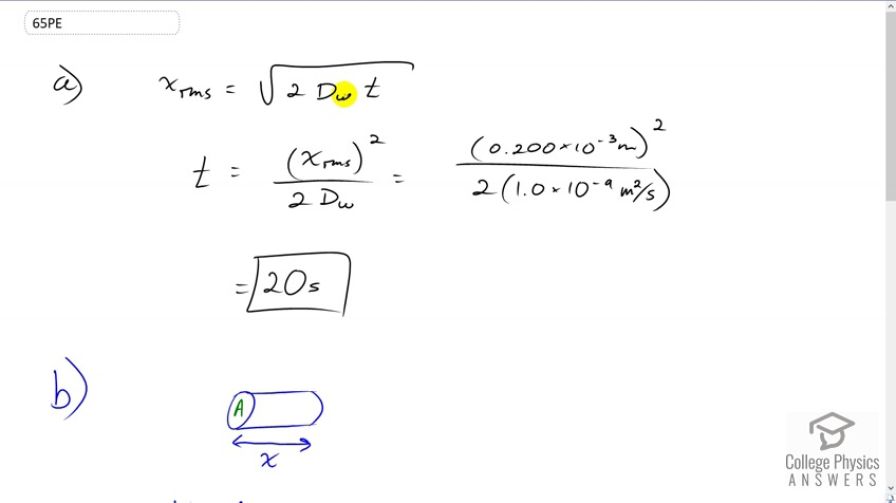
vote with a rating of
votes with an average rating of
.
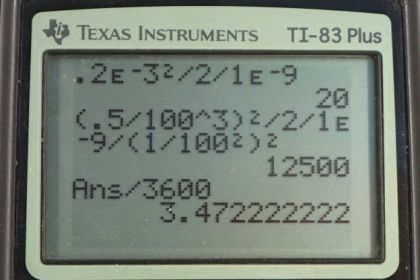
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. The average distance that an Oxygen molecule will diffuse through water, is going to be a square root of two times the diffusion constant of Oxygen and water times time. So, if we both square both sides and then divide both sides by two Dw, we'll solve for t. So t is going to be the average distance squared over two times the diffusion constant. That's 0.2 times ten to the minus three meters squared divided by two times 1.0 times ten to the minus nine meters squared per second. This gives about 20 seconds. So we'll take 20 seconds for an Oxygen molecule to diffuse, about 0.2 millimeters in tear layer which is made up of water. Now in part b, we're asked how long it takes to diffuse 0.3 cubic centimeters of oxygen given the surface area of the cornea of one square centimeters? Basically, we're asking how long will that take to diffuse Oxygen through this cylinder with a given volume of the cross-sectional area multiplied by the length of the cylinder which is going to be the distance the Oxygen travels x. And so we'll use this formula for the average distance of diffusion and substitute that in for x. And so we have V equals area times square root two diffusion constant times time and then we'll divide both sides by A. And so we have this line here and then square both sides, we get two times diffusion constant times time equals volume squared over area squared and then divide both sides by two times the diffusion constant. And so the time will be the volume squared divided by two times the diffusion constant times the area squared. So that's 0.5 cubic centimeters, which we have to write in cubic meters in order to have consistent units with this diffusion constant here. So we multiply it by one meter for every 100 centimeters three times and then square that result and divide by two times 1.0 times ten to the minus nine meters squared per second times one square centimeter of area converted into meter squared and we square that result. And this works out to three and a half hours.