Two parallel plate capacitors are otherwise identical, except the second one has twice the distance between the plates of the first. If placed in otherwise identical circuits, how much charge will the second plate have on it compared to the first? (a) four times as much
(b) twice as much
(c) the same
(d) half as much

Video Transcript

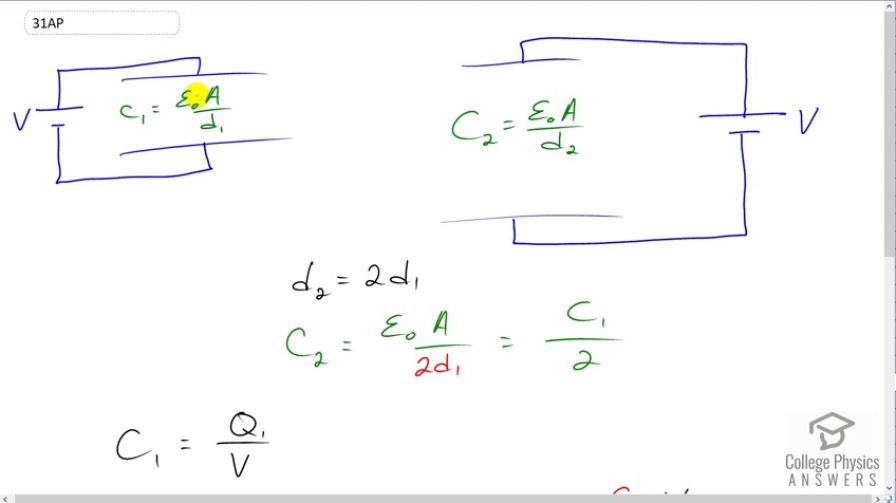
This is College Physics Answers with Shaun Dychko. We have two parallel plate capacitors here. And the first one, we'll call it capacitor one, has a capacitance of permittivity free space times the area divided by this distance one separating the two plates. And then, case two, that's going to be the same permittivity of free space times the same area, because we're told the capacitors are identical, except that their separation between the plates are different. And, it's going to be divided by D two. Now, we're told that this distance two separation of the plates is going to be two times the distance in the first case. And so, when we're looking for capacitance two, we can substitute two D one in place of D two, and we have these all here, is C one, and so we can write is as C one divided by two. So, capacitance two is half of capacitance one. Now, we're going to compare the amount of charge accumulated on each capacitor when they are put in identical circuits. So, that means that the voltage will be the same for both circuits. So, there's no need for a subscript one or two here, because these voltages are the same. So, in the case of capacitor one, it's going to accumulate this much charge, Q one, divided by V. And we can solve for Q one by multiplying both sides by V, and we have Q one is C one V. And Q two, by the same algebra, would be C two times V, but C two, we know is C one over two, so we can replace that here. And so now, we can see that Q two is half of Q one, because C one V is Q one, so we can write Q one over two, which I wrote here. And so, capacitor two has accumulated half the charge that capacitor one has, and that is option D. Here. There we go. Half as much.