Question
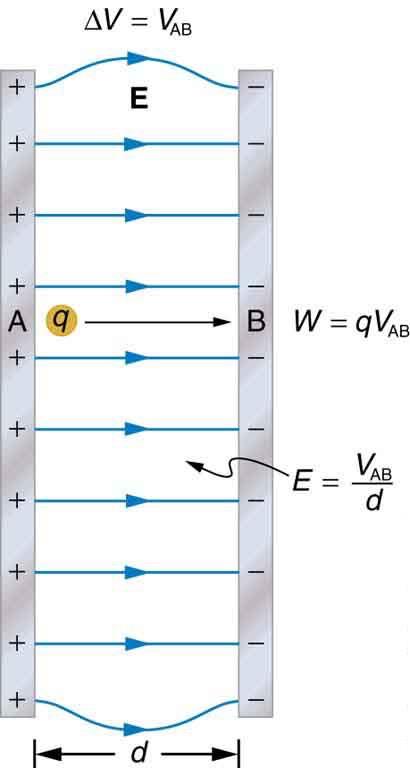
A negatively charged massive particle is dropped from above the two plates in Figure 19.7 into the space between them. Which best describes the trajectory it takes?
- A rightward-curving parabola
- A leftward-curving parabola
- A rightward-curving section of a circle
- A leftward-curving section of a circle
Final Answer
The correct answer is that the electron will follow a straight line path down and to the left. This, unfortunately, isn't one of the options provided. In a case like this you have to (after taking a deep breath to quell frustration) choose the best wrong answer. The best wrong answer is (b). See the solution video for details.
Solution video
OpenStax College Physics for AP® Courses, Chapter 19, Problem 17 (Test Prep for AP® Courses)
vote with a rating of
votes with an average rating of
.
Video Transcript
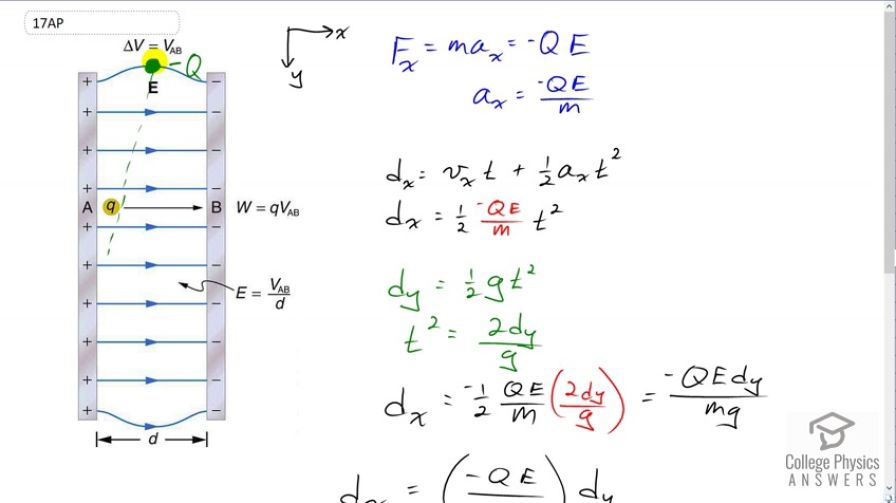
This is College Physics Answers with Shaun Dychko. We have two vertical parallel plates with opposite charges and electric field pointing to the right between them and then there is a negative charge position in the centre at the top here and it is dropped, and the question is what shaped path will it follow as it goes down through this electric field. So, we have to, well we want to figure out what the forces are on in the x direction and based on that force figure out its acceleration in the x direction and knowing it acceleration find its x-position as a function of time and then we can find the y-position as a function of time and then solve for time and substitute that back into the equation for x-position and then we will get an x-position with respect to the y-position and so having the x-position with respect to the y-position will tell us the shape of this path, coz it tell us where it is horizontally speaking for every position vertically speaking, okay. So, and I also have made a spreadsheet describing the path that it is taking which is a straight line by the way and that’s a bit of a surprising answer based on the options given to us by the question since straight line is not one of the option mentioned. As you can see from the option here, right curving parabola, left curving parabola, right curving section of a circle or left circle. So, lets figure out what’s actually going on though. Now, the force on this particle in the x-direction, the net force will be mass times the acceleration in the x-direction and its going to be the force due to electric field which will be this, charge negative Q multiplied by the electric field strength and we will solve for acceleration by dividing both sides by m. So, we have a x equals negative Q E over m. Now, the x-position as a function of time will be the initial x-velocity times time which there is none so that term is zero since there is no initial x-velocity plus one half times x-acceleration times time square. This is gonna work in pneumatic formulas and we are going to substitute for a x by writing negative Q E over m in its place. So, the x-position is one half negative Q E over m times time squared. Now, that’s not good enough, we don’t want to have time in our equation, we want to have the y-position. So, consider the y-position then, its gonna be one half times acceleration due to gravity times squared and we can solve for time square by multiplying both sides by two over g and we get t squared is two d y over g and that is what we plug-in for time squared in our d x formula and after you cancel this two with this one half, you get negative Q E d y over m g. Now, all of these things are constants and so we can just group them together and this is of the form of a linear equation. This is a straight-line formula, its of the form y equals m x plus b where the y-intercept is 0 and the slope is negative Q E over m g. Don’t take the negative too seriously though, this is typically the, typically a positive slope but to find my coordinate system with positive or y in the downward direction. So… Now, that’s enough to say that the path will be a straight line but if you don’t quite believe it, we can use a spreadsheet too to calculate what the positions will be. So, I have created some hypothetical charges, electric field strength and mass and created some hypothetical time here and the formula for the x-position as one-half times charge multiplied by electric field strength divided by the mass and then multiplied by time squared. A7 is the reference to this cell to the left of B7 and that’s following this formula here. I guess I forgot to put a g in here actually, I should put a 9.8 in there and, Ta-Da, times 9.8 but well, doesn’t really matter but will do anyway I guess. So, and we copy this data, its not gonna change the shape of the graph, so its not really that important to do this but its going to change the numbers on the graph anyhow, okay and formula didn’t copy up to this point here, it’s an outlier, so lets copy it down there. Good. Still a straight line and the y-position is going to be negative half times 9.8 times the time squared and that’s, this formula here Oh, you know what, apologies, there is no g in this formula coz we are dealing with time squared that was thinking more along lines of this formula but that’s not what we are using here, we are using the formula in terms of time squared for both of them so this is one formula we are using and this is the other. This is the column for d x and this is the column for d y so infact this 9.8 doesn’t need to be there. I am using the program called LibreOffice by the way, it’s a free spreadsheet program like Microsoft excel, just free and we can see that this is a straight line and without any doubt none of the answers are given to us by the textbook are correct and so the next thing you do when you encounter a situation is to choose the least wrong answer, the best answer you could say and probably what they are looking for, well, certainly leftward is without a… something looking for because Q being the negative charge and the field pointing toward the right, there is going to be a path, this is going to move left so that knows a down to b or d and since some of our equations involve time squared likely the person who made the exam is thinking about the parabola and so b is the best wrong answer but the real answer is straight line to the left.