Question
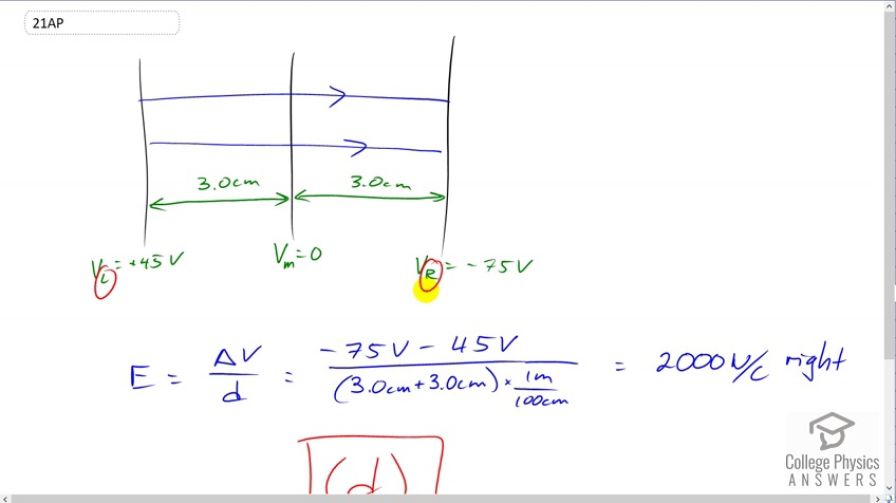
Consider three parallel conducting plates, with a space of 3.0 cm between them. The leftmost one is at a potential of +45 V, the middle one is held at ground, and the rightmost is at a potential of -75 V. What is the magnitude of the average electric field on an electron traveling between the plates? (Assume that the middle one has holes for the electron to go through.)
- 1500 V/m
- 2500 V/m
- 4000 V/m
- 2000 V/m
Final Answer
(d)
Solution video
OpenStax College Physics for AP® Courses, Chapter 19, Problem 21 (Test Prep for AP® Courses)
vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. This question asks us for the average electric field between the first and last plate, the left hand plate and the right hand plate, L for left and R for right. And, it puts a third plate, I'll call it V subscript M for middle, in between the two equidistant from the right and left plates, three centimeters in each side. And, they've chosen numbers here conveniently such that the middle plate actually doesn't matter at all. Both of these voltages for the left and right plates are both measured with respect to the middle plates, since the middle plate has a voltage of zero, and this is 45 volts above zero, and this is 45 volts below zero. And, since this plate is equidistant, then we're taking the average, that means we can just ignore it entirely. If this plate was not in the middle, then we would take a distant weighted average of the electric fields of both sides of the middle plate. If it was here, for example, and it was 1 centimeter separated from the left plate, and then therefore, give centimeters from the right, then we would find the electric field here, multiplied by one-sixth, because of the total of six centimeters, and then find the electric field here and multiply it by five-sixths. And then, combine the two or take the average of the two that way, in a weighted form. You take this electric field multiply it by one-sixth plus this electric field multiplied by five-sixths would be the answer to our average electric field. That would be weighted average, distance weighted average. But in this case, since the distance is the same on both sides, there's no need to do the calculation. We can just take the final voltage here minus the initial voltage there, and divide by the total distance converted into meters. And, we end up with 2000 Netwons per Coulomb. And, this is to the right because this is the positive plate, and this is the negative plate, and electric field lines always emanate from positive towards negative. The answer is D in our listed possibilities for this question.
