A parallel plate capacitor with adjustable-size square plates is placed in a circuit. How does the charge on the capacitor change as the length of the sides of the plates is increased? (a) it grows proportional to ${\text{length}}^2$
(b) it grows proportional to length
(c) it shrinks proportional to length
(d) it shrinks proportional to ${\text{length}}^2$

Video Transcript

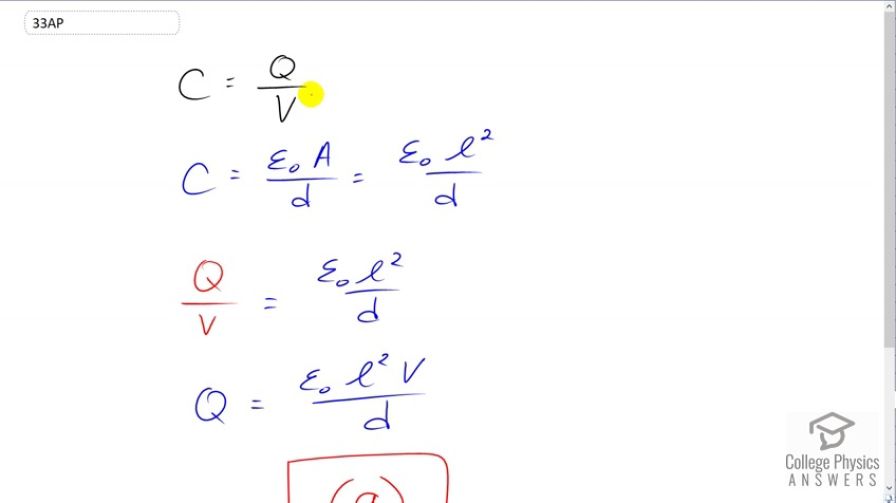
This is College Physics Answers with Shaun Dychko. Given a parallel plate capacitor with square plates, we're going to find out how the amount of charge accumulated on the capacitor changes with the side length of the plates. So, capacitance is the amount of charge accumulated divided by the voltage of the circuit. And, for a parallel quick capacitor, that's going to be permittivity of free space times the area of the plate divided by the separation between plates. And, the area, given that this is going to be square plates, will be the side length squared. And so now, we have two expressions for the capacitance, this one and this one, and so we can equate them. So Q over V equals Epsilon naught L squared over D, and we'll solve for Q by multiplying both sides by V. So, Q is permittivity of free space times the side length squared times V over D. And that means that the amount of charge accumulated increases with the square of the side length. And, that is option A.