Question
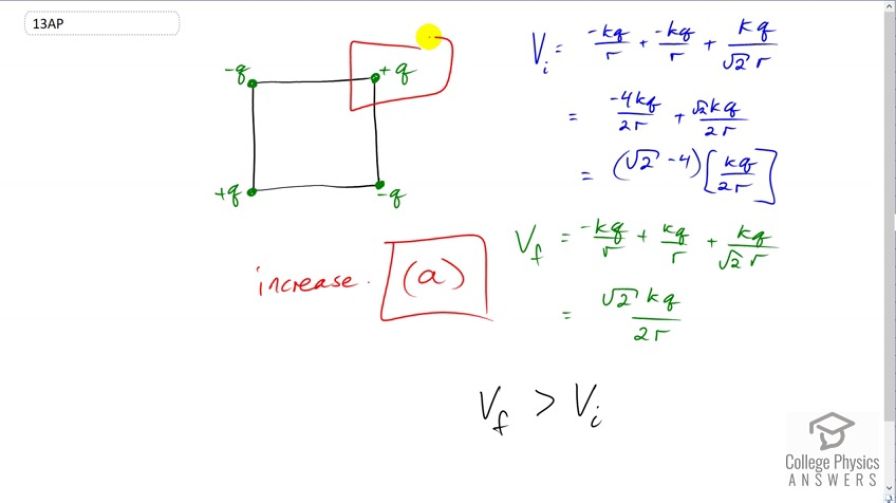
Take a square configuration of point charges, two positive and two negative, all of the same magnitude, with like charges sharing diagonals. What will happen to the internal energy of this system if one of the negative charges becomes a positive charge of the same magnitude?
- increase
- decrease
- no change
- not enough information
Final Answer
(a)
Solution video
OpenStax College Physics for AP® Courses, Chapter 19, Problem 13 (Test Prep for AP® Courses)
vote with a rating of
votes with an average rating of
.
Video Transcript
This is College Physics Answers with Shaun Dychko. So, there is a quick and a slow way to answer this question. Let’s do the quick way first, so we are gonna consider the energy of this particular charge and we will use that as a way of thinking about the energy of the whole system. So, the energy of this charge will be, its charge multiplied by the potential of this position and this potential is due to the other three charges and positive charges create positive potential and negative charges create negative potential. So, the more positive charges are, the more potential will be at this position and so by switching from the negative charge to a positive charge like this, that’s going to increase the potential of this corner and so its gonna increase the internal energy of the system, so that’s the quick way to think about it. Bit of a slower way is to actually calculate the potential at this position and so initially when you have two negative charges and a positive on the diagonal, the potential is going to be negative k q over r due to this charge here and the side length is r by the way and then plus another negative k q over r and, yep, plus k q over this diagonal distance here which is you know using Pythagoras’s, the square root of r squared plus r squared which is the square root of two r square which can be written as root two r and that’s what I have here and then combine these two like-terms and you get negative four k q over two r making two the common denominator by multiplying top and bottom by two here and then adding the numerator, two plus two making four, there’s a negative four and in this one get multiplied by root two over root two just because you know when you are simplifying radicals, You've meant to have no radicals in the denominator of a fraction, so I wrote a root two k q over two r and then k q over r can be factored out or k q over two r should say and you get root two minus four time k q over two r as potential initially when you have two negative charges. Now, if one of the charges switches to positive, we will have a final potential of negative k q over r plus positive k q over r plus the same k q over root two r and these make zero and so our final potential is root two k q over two r and root two k q over two r is greater than root two took away this four times the same factor, k q over two r and so the final potential is greater than the initial potential. This is definitely going to cause an increase in the internal energy of the system, the answer is A.