Question
In some countries, liquid nitrogen is used on dairy trucks instead of mechanical refrigerators. A 3.00-hour delivery trip requires 200 L of liquid nitrogen, which has a density of . (a) Calculate the heat transfer necessary to evaporate this amount of liquid nitrogen and raise its temperature to . (Use and assume it is constant over the temperature range.) This value is the amount of cooling the
liquid nitrogen supplies. (b) What is this heat transfer rate in kilowatt-hours?
(c) Compare the amount of cooling obtained from melting an identical mass of ice with that from evaporating the liquid nitrogen.
Final Answer
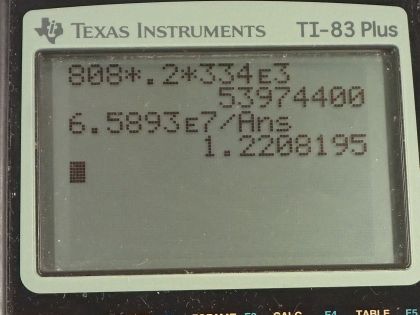
- Liquid nitrogen has a cooling effect 22% greater than that of an equal mass of melting ice.
Solution video
OpenStax College Physics, Chapter 14, Problem 28 (Problems & Exercises)

vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. We are going to look into the cooling effect of liquid nitrogen; imagine that some liquid nitrogen is cooling for a period of 3.00 hours and it has an initial volume of 200 liters which we convert into 0.200 cubic meters. It has a density of 808 kilograms per cubic meter and a specific heat capacity when it's kept at constant pressure— which means the gas is allowed to expand which it would in a dairy truck— of 1040 joules per kilogram per Celsius degree and this figure comes from our data table— right here for 'Nitrogen'— and the number in brackets is the one to use for constant pressure and the one without brackets is for when there's constant volume. You don't have these distinctions when you are dealing with liquids or solids because these things are not gonna be changing their volume or pressure with temperature but the nitrogen, as it heats up, it will increase its volume and thereby keep a constant pressure and so this is the figure to use in that scenario. Okay! We are gonna assume that the liquid nitrogen begins at its melting point which is minus 195.8 degrees Celsius and is raised up to a temperature of 3.00 degrees Celsius and the latent heat of vaporization for nitrogen to change its phase from liquid into gas is 201 times 10 to the 3 joules per kilogram. Okay! So the amount of heat that the liquid nitrogen can absorb is its mass times its latent heat of vaporization plus that same mass, which is now in gaseous state, increasing its temperature from its melting point up to 3.00 degrees Celsius. And we can factor out the m here and so we have m times latent heat of vaporization plus specific heat capacity at constant pressure times the final temperature minus the initial temperature. Now we are not given what the mass is but we are given the density and the volume so we know that density is mass divided by volume and we can solve for m by multiplying both sides by V and now this is something we can plug in for m so m is density times volume and so I have made a substitution for m here... then we plug in numbers. So the amount of heat it can absorb is 808 kilograms per cubic meter times 0.200 cubic meters times 201 times 10 to the 3 joules per kilogram— latent heat of vaporization— plus 1040 joules per kilogram per Celsius degree— specific heat at constant pressure— times 3.00 degrees Celsius—final temperature— minus negative 195.8 degrees Celsius— initial temperature— and this is 6.59 times 10 to the 7 joules of heat energy absorbed. Now in part (b), we want to convert this into units of kilowatt-hours and so we take this number of joules, divide it by the time but we have to convert the time into seconds in order to get watts between these two parts and then we convert the watts into kilowatts and this will be watts because it ends up with units of joules per second since the hours here cancel and now we have kilowatts once we get to this point and then we multiply the kilowatts by the number of hours which is 3 hours and we end up with kilowatt-hours so that's 18.3 kilowatt-hours. Now we are going to find the equivalent amount of heat that would have been absorbed by changing 0 degree ice into water with the same mass of ice as we started with nitrogen. And so we'll replace this mass of water times the density of nitrogen multiplied by the volume of nitrogen we are working with and we are multiplying by the latent heat of fusion for water. So it's 808 kilograms per cubic meter times 0.200 cubic meters times 334 times 10 to the 3 joules per kilogram and that's 5.397 times 10 to the 7 joules. So to make a comparison, we could divide them. So we'll divide the amount of heat absorbed by the nitrogen by the heat absorbed by the water while changing from ice to water and this is 1.22. So this represents a 22 percent greater cooling effect from liquid nitrogen than from an equal mass of melting ice.