Question
On a certain dry sunny day, a swimming pool’s temperature would rise by if not for evaporation. What fraction of the water must evaporate to carry away precisely enough energy to keep the temperature constant?
Final Answer
Solution video
OpenStax College Physics, Chapter 14, Problem 16 (Problems & Exercises)
vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
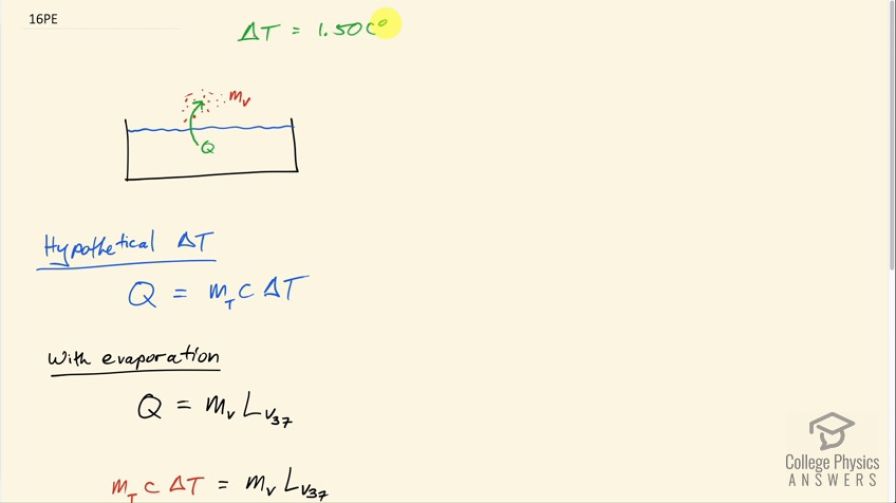
This is College Physics Answers with Shaun Dychko. We are told that on a sunny day, a swimming pool would hypothetically increase its temperature by 1.50 Celsius degrees. Now it's just hypothetical because we are told that suppose that instead of that temperature increase, there is that same amount of heat put into evaporation or some amount of water vaporizing and so figure out what fraction of the water needs to vaporize in order to maintain a constant temperature which is to say that all the heat absorbed from the Sun is turned into this this vaporization or causes this vaporization. Okay! So in the hypothetical change in temperature, it would take an amount of heat equal to the total mass of the water times its specific heat of water times the change in temperature. Now with evaporation, the phase change of evaporation will absorb an amount of heat equal to the mass of water that vaporizes times the latent heat of vaporization and we use the value for this for water at 37.0 degrees Celsius because that's a better approximation to the temperature involved in this question than the 100.0 degrees Celsius that is in our data table here. So we won't use this number... instead we'll use 2430 times 10 to the 3 joules per kilogram. Okay! So all this heat in the hypothetical temperature change is equal to this heat absorbed to cause evaporation and we can solve for m V divided by m T which will be the fraction in mass terms of the water that needs to evaporate. So we'll divide both sides by m total and also divide both sides by this latent heat of vaporization at 37.0 degrees and we end up with m V over m T is cΔT over < i>L V 37. So that's 4186 joules per kilogram per Celsius degree— specific heat of water which we found here— and then multiply that by 1.50 Celsius degrees— hypothetical temperature change— divided by this latent heat of vaporization at 37.0 degrees. So I erased a little mistake there that had grams; it's not the mass that we are finding that vaporizes, it's the fraction of the total that we are finding that vaporizes. So this is 2.58 times 10 to the minus 3 is the fraction of water that needs to evaporate in order to maintain a constant temperature.
