- please see the graph in the solution video.
Solution video
OpenStax College Physics, Chapter 14, Problem 17 (Problems & Exercises)

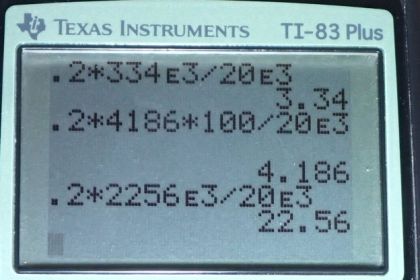
Calculator Screenshots
Comments
Absolutely no where online can i find the the latent heat of fusion of ice that is the SAME as the value shown above. they're all rewritten in different units of measurements, which you dive into an explanation upon that
Hi JPengson, thank you for your question. Yes, there's a lot of data to keep track of in these questions. The latent heat of fusion is in section 14.3 in the OpenStax textbook, where you'll find 334 kJ/kg, which converts to 334,000 J / kg or it's written in the video as . Wikipedia gives a more precise value of 333.55 J/g which converts to (notice the numerical value didn't change since it was both multiplied and divided by 1000 during the conversion). The Wikipedia value rounds to the same value as given by OpenStax.
Keep in mind that the value of is the specific heat of ice given in section 14.2.
Hope this helps,
Shaun