Question
Many decisions are made on the basis of the payback period: the time it will take through savings to equal the capital cost of an investment. Acceptable payback times depend upon the business or philosophy one has. (For some industries, a payback period is as small as two years.) Suppose you wish to install the extra insulation in Exercise 14.41. If energy cost $1.00 per million joules and the insulation was $4.00 per square meter, then calculate the simple payback time. Take the average for the 120 day heating season to be .
Final Answer
The payback period is 0.26 years, not including installation costs.
Solution video
OpenStax College Physics, Chapter 14, Problem 43 (Problems & Exercises)
vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
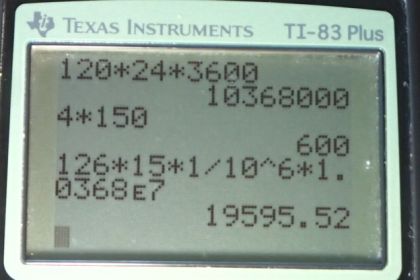
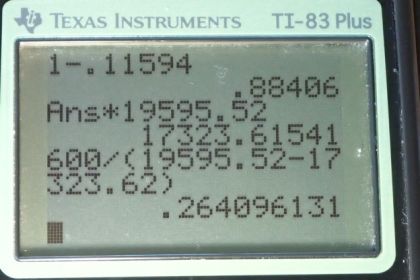
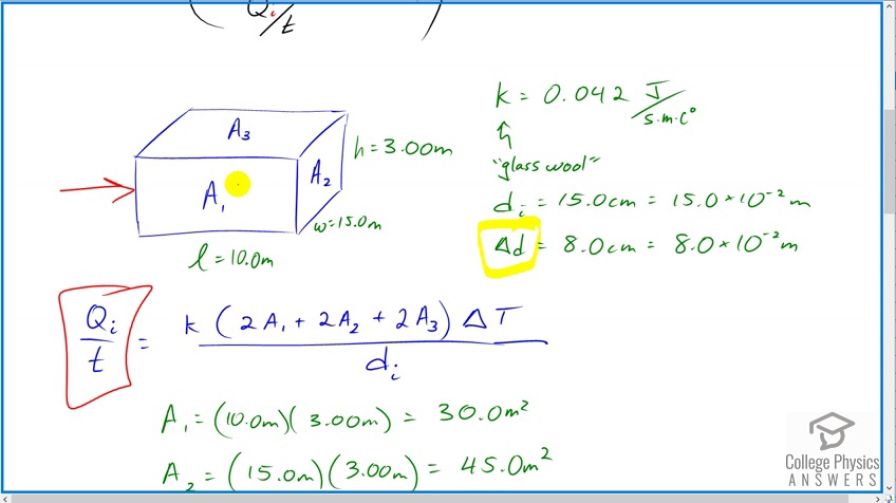
This is College Physics Answers with Shaun Dychko. In this question, we are considering the house of problem 41 which I drew here and has side length of 10, 15 and 3 meters high some extra insulation is being added to the attic and that’s causing the rate of heat transfer to change from 126 watts per Celsius degree multiplied by the temperature difference to a final rate of heat transfer of this, 111.391 times the change in temperature difference, after the insulation is added. So, the rate of heat transfer is decreasing as a result of this extra 8 centimetres of insulation added to the attic. So, we are told that the the rate at which the electricity cost is 1 dollar for every 10 to the 6 joules, so a dollar per megajoule and the cost for insulation, you know the rate of which insulation cost is, that’s why have r there. It's kind of a rate, it's something per something else. It's four dollars per square meter. Now, we will figure out what the additional cost for adding the insulation to the attic is and then we will see what period of time the savings in energy costs will add up to that cost of the extra insulation, that’s the payback time. So, the time during which energy is being lost, the heating season is a 120 days every year and we multiply that by 24 hours per day times 3600 seconds per hour to get 1.0368 times 10 to the 7 seconds per year. So, this is the duration of heating. So, this is the time over which heat is being lost per year and this is the time during which we are paying this bill, this 1 dollar per 10 to the 6 joules and the temperature difference we are told is 15 Celsius degrees and so we can use that to turn this rate of heat loss into watts. So the capital cost here is the cost of the insulation and so we are adding, this insulation, it's gonna be four dollars for every square meter and it's being multiplied by the area of the attic or ceiling which is a 150 square meters and so that’s 600 dollars. So, 600 dollars has been paid to add extra insulation. Now, the cost per year initially is going to be the rate of heat transfer initially multiplied by the cost, the electricity cost, multiplied by the time period over which this is happening. So, this is 126 watts per Celsius degree multiplied by difference in temperature, that’s the substitution in place of Q i over t and then we multiply that by the cost times the period. So, that’s 126 times 15 times a dollar for every 10 to the 6 joules and the units of this will be, all those Celsius degrees will cancel and this is going to be joules per second and we are dividing by joules, so this is a per second unit and then we are multiplying by seconds per year so this is going to be dollars per year in the end and this works out to 19595 dollars and 52 cents every year and then the final cost per year, well, we know that the the rate of heat transfer is 12 percent less and so the final cost is going to be 1 minus that 12 percent which I have written with lots of digits instead of just rounding it to 12 and then we multiply that by the cost per year that we just calculated here and we get 17323 dollars and 62 cents. If you prefer, you don’t have to calculate it this way. We could have instead calculated it as the same way as we did for the initial cost per year and substituted 111 point something something there, 111.391 and multiplied by 15 times a dollar per 10 to the 6 joules times this many seconds per year, we could have done that to calculate this number as well. Okay and then taking this difference, this is the difference in cost per year times some period T, which is number of years has to equal 600 dollars. So this cost savings times some period of time the payback period is going to equal 600 dollars and so we divide both sides by this difference to isolate T and so T is 600 divided by the savings per year and this works out to 0.26 years and this is not including installation cost of course, just the cost of the materials. But in one quarter of a year, the extra cost of the insulation becomes worth it in savings on the electricity bill.