Question
Hot air rises because it has expanded. It then displaces a greater volume of cold air, which increases the buoyant force on it.
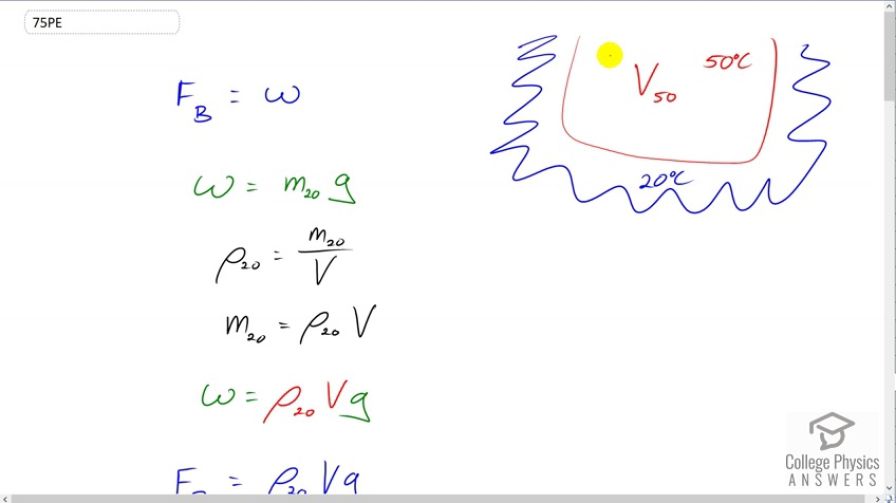
- Calculate the ratio of the buoyant force to the weight of air surrounded by air.
- What energy is needed to cause of air to go from to ?
- What gravitational potential energy is gained by this volume of air if it rises 1.00 m? Will this cause a significant cooling of the air?
Final Answer
Solution video
OpenStax College Physics, Chapter 14, Problem 75 (Problems & Exercises)
vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. Some 50 degree air is surrounded by 20 degree air. And, our question is to find the ratio of the buoyant force on the hot air to its weight, the weight of the hot air. So, the buoyant force is equal to the weight of the fluid displaced by the thing that is submerged. So, you can imagine that this hot air is submerged so to speak in this cold air. And so, we need to find the weight of the cold air that was displaced by this hot air. So, that'll be the mass of the cold air displaced multiplied by G. Acceleration due to gravity or gravitational field strength. And, now we don't know what the mass is, but we can figure out the volume because we're given the volume of the 50 degree air, and that will be the same as the volume displaced. It'll displace an amount of 20 degree air equal in volume to the size of the thing, the thing being this hot air. So, the density of the 20 degree air is the mass of the 20 degree air divided by its volume. I did not put a subscript on the volume for the 20 degree air because the volume of the 20 degree air displaced is the same as the volume of the 50 degree air and so there's no need for a subscript. Now, we'll solve this for M 20, the mass of the 20 degree air by multiplying both sides by V, and that gives us this expression which we can substitute in for M 20. So, the weight of the fluid displaced by the hot air, and I mean fluid in a more general sense to include air in gases. So, the weight of the 20 degree air displaced is the density of the 20 degree air multiplied by its volume times G. So, this can all be written in place of W in this Archimedes' Principle formula to say that the buoyant force equals density of 20 degree air times its volume times G. Now, we want to take this buoyant force and divide it by the weight of the 50 degree air. So, let's find out the weight of the 50 degree air now. And, with the same sort of reasoning up here, it's going to be the density of 50 degree air times its volume times G. And, now we divide these two things. So, divide this by this and we get this expression and the volumes and G's cancel. And, we're left with the density of the 20 degree air divided by the density of the 50 degree air. And, now we don't know what these densities are but we do know temperatures. So, it turns out that this ratio is going to be the ratio of the temperatures. So, we can use this ideal gas law, which says pressure times volume equals the number of moles of the gas times universal gas constant R times its absolute temperature. And, we'll solve this for V and we'll substitute that into our density formula. Now this is density of 20 degree or 50 degree air. It is just density in general for a gas. Now, pressure we can assume is going to be constant in this question because it's all in the atmosphere here and if there is much pressure difference, then there will be wind blowing and high pressure would move towards low pressure and so for a situation like this to sustain for a little while, it's going to have to not have any pressure differences. So, assume pressure is constant. I mean, there are lots of assumptions in this question, really. Even assuming that G is constant is a bit of an assumption because Nah, never mind. That's a pretty good assumption because they're both at the same distance from the center of the earth. Never mind. Okay. So, let's not digress too much. Density is mass divided by volume. So, let's divide by this. Because we want to express things in terms of temperature since that's the information we know, we can't go look up the density of air in a data table because density of air, which is about 1.29 kilograms per cubic meter, this value is at standard temperature and pressure. And, these are not standard temperatures. This is 20 degrees Celsius and this is 50 degrees Celsius. Standard temperature is 0 degree Celsius. So, we can't resort to that. And so, we have to think of something different, which is to consider that density is mass divided by volume. And, we'll divide by this, which is the same as multiplying by its reciprocal. So, we have mass times pressure over number of moles times universal gas constant times temperature. And so, we can express density in this way in terms of T. Okay. So then, the mass, also, we want to get rid of because we don't know what that is either and it's going to be the number of moles of the gas times the molar mass of the gas. And, this molar mass is kind of a chemistry concept but think of it as the number of grams in a mole of this gas mixture, which will contain nitrogen, oxygen, little bit of CO2 and so on. Okay. So, we plug that in for M and we get this. And that's useful because now these number of moles cancels and we didn't know what that was anyway, so that's good that it cancels. And then we have all of this. Molar mass times pressure divided by the universal gas constant times temperature. So, now we can rewrite this buoyant force to weight expression as the ratio of densities, but instead of densities, we're going to substitute this. So, we have the density for the 20 degree air is molar mass times pressure divided by gas constant times the temperature of this one, the 20 degree air. And then, we'll divide that by the density of the 50 degree air but using this expression in place of density. Now, dividing by this fraction is the same as multiplying by its reciprocal. So, we're going to write R T50 over M P. And then a whole bunch of things cancel. And, we're left with T50 over T20. So, the ratio of the buoyant force to the weight, then, is going to be 50 degrees divided by 20 degrees but expressing both of those in absolute temperatures, by adding 273.15. And, we get 1.10 is the ratio of the buoyant force to the weight. Alright. Part B is asking what energy is needed to cause a cubic meter of this area to go from 20 to 50 degrees Celsius. So, the energy that will be absorbed is going to be the mass of the air times the specific heat of air times the change in temperature. And, we don't know what the mass is. We do know volume, and so we will express all of this in terms of density. So, density is mass divided by volume. And, we'll solve for M by multiplying both sides by V and then we will substitute this in place of M. So, the amount of energy that will be consumed to increase the temperature of the air will be its volume times the density times the specific heat times change in temperature. And, we are using this 1.29 kilograms per cubic meter because that's the best estimate we can get in this circumstance for the density. And, the actual density will be somewhere close to this, anyway. And so, we put in 1.29 there times a cubic meter times 721 Joules per kilogram per Celsius degree times the change in temperature, which is the difference between 50 and 20, and this gives 2.79 times 10 to the 4 Joules of thermal energy required to increase a cubic meter of air in temperature from 20 to 50. The amount of gravitational potential energy that a cubic meter of air would gain as it increases in height of one meter will be its mass times gravitational field strength times the change in height. And, mass is volume times density, as we said up here. And, we'll substitute that. And so, we have a cubic meter times 1.29 kilograms per cubic meter density times 9.81 newtons per kilogram gravitational field strength times one meter increase in height, which is 12.7 Joules. Now, this energy must come from somewhere because energy cannot be just created out of nothing. That's the conservation of energy law for which no exception has ever been noticed ever. So, this gravitational potential energy is going to come from thermal energy of the air because the air is going upwards because of temperature differences which are causing density differences and thereby causing their buoyant force. So, it turns out that it would not take very much thermal energy to impart this amount of gravitational potential energy because 12.7 Joules is much much less than 2.79 times 10 to the 4 Joules. And, there we go.

