Question
A bag containing 0∘C0^\circ\textrm{C} ice is much more effective in absorbing energy than one containing the same amount of 0∘C0^\circ\textrm{C} water. a. How much heat transfer is necessary to raise the temperature of 0.800 kg of water from 0∘C0^\circ\textrm{C} to 30.0∘C30.0^\circ\textrm{C}? b. How much heat transfer is required to first melt 0.800 kg of 0∘C0^\circ\textrm{C} ice and then raise its temperature? c. Explain how your answer supports the contention that the ice is more effective.
Question by OpenStax is licensed under CC BY 4.0
Final Answer
  1. 1.00×105 J1.00\times 10^{5}\textrm{ J}
  2. 3.68×105 J3.68\times 10^{5}\textrm{ J}
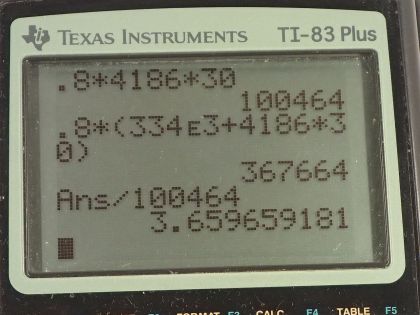
  3. Melting the ice before increasing the temperature of the water increased the heat absorbed by a factor of 3.7. Starting with ice is much more effective at absorbing heat.

Solution video

OpenStax College Physics, Chapter 14, Problem 12 (Problems & Exercises)

OpenStax College Physics, Chapter 14, Problem 12 (PE) video thumbnail

In order to watch this solution you need to have a subscription.

Start free trial Log in
vote with a rating of votes with an average rating of .
Chevron left Prev
Select problem
Next Chevron right

Calculator Screenshots

  • OpenStax College Physics, Chapter 14, Problem 12 (PE) calculator screenshot 1
Video Transcript
This is College Physics Answers with Shaun Dychko. We are going to compare the absorption of heat energy between a bag of water, which starts at 0.0 degrees Celsius, and compare that to the same bag but with ice in it first which also has a temperature of 0.0 degrees Celsius. So the only difference is that one starts as liquid and the other starts as ice; they both start with the same temperature of 0.0 degrees Celsius. So we have gathered some information here: the question tells us we are dealing with 0.800 kilograms of water or ice; the specific heat of water we look up in our data tables here and it's 4186 joules per kilogram per Celsius degree and the latent heat of fusion for water is 334 kilojoules per kilogram so I'll write that as 334 times 10 to the 3 joules per kilogram. So in part (a) we have just water and it's going to absorb an amount of heat equal to its mass times its specific heat times the change in temperature. So that's 0.800 kilograms times 4186 joules per kilogram per Celsius degree times 30.0 degrees Celsius— final temperature— minus 0.0 degrees Celsius— initial temperature— and that is 1.00 times 10 to the 5 joules of heat energy will be absorbed. In part (b), we have that same amount of heat energy needed to change its temperature but before that, we also are going to absorb some energy due to melting the ice and that will be an amount of its mass multiplied by its latent heat of fusion. So m is a common factor between these two terms so we can factor it out and we have m times latent heat of fusion plus specific heat times change in temperature. So that's 0.800 kilograms times 334 times 10 to the 3 joules per kilogram plus 4186 joules per kilogram per Celsius degree times 30.0 degrees Celsius and that is 3.68 times 10 to the 5 joules. So this shows that starting with ice is much more effective because it will absorb additional heat just to melt the ice. It will absorb an amount of heat that is increased by a factor of 3.7; if you take the amount of energy with the ice melting first divided by the scenario where they are just starting with water, 3.7 times as much energy is absorbed when starting with ice.